Souffre radioactif

Dans cette vidéo, on étudie l'utilisation possible du soufre radioactif en tant que traceur biologique. L'isotope radioactif du soufre 38 est utilisé pour étudier le métabolisme des protéines. On commence avec un échantillon de protéines marqué avec cet isotope, qui a une activité initiale de 4,8 x 10^4 désintégrations par minute. On souhaite calculer l'activité de cet échantillon après 8 heures et 24 heures. 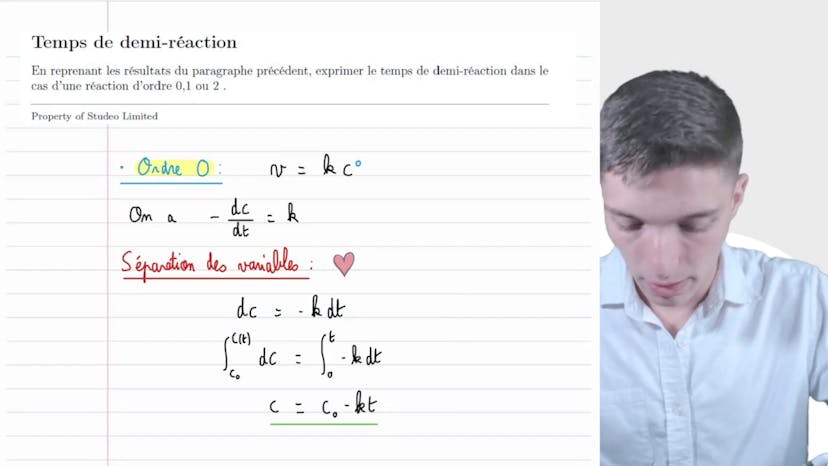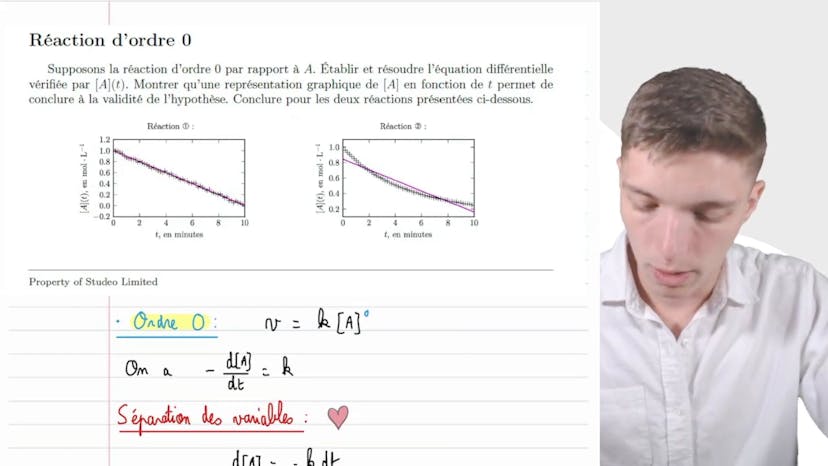Pour résoudre ce problème, on utilise la décroissance exponentielle de l'isotope radioactif. On pose une expression pour la concentration en isotope en fonction du temps, en utilisant la concentration initiale et la constante de décroissance. On utilise également la définition de la demi-vie, qui indique que la concentration à n'importe quel instant est égale à la concentration initiale divisée par deux après une durée de demi-vie. En résolvant l'équation obtenue, on détermine la constante de décroissance alpha, qui permet ensuite d'exprimer la loi de concentration de l'isotope. On peut alors calculer la vitesse de décroissance en utilisant la dérivée temporelle de la concentration. Cependant, on dispose de l'activité initiale de l'échantillon, qui est la vitesse de disparition de l'isotope, plutôt que de sa concentration initiale. On calcule donc la vitesse initiale en utilisant cette activité. On peut ensuite utiliser toutes ces informations pour calculer l'activité de l'échantillon après 8 heures et 24 heures. En effectuant les calculs numériques, on obtient une activité de 6812 désintégrations par minute après 8 heures et 137 désintégrations par minute après 24 heures. Malgré la complexité de cet exercice, il est important de prendre des initiatives et d'essayer différentes approches pour résoudre le problème. Même si on se trompe, cela permet de progresser et de trouver la bonne solution. Il faut donc se lancer, être confiant et ne pas avoir peur de se tromper. Merci d'avoir suivi cette vidéo et à bientôt !