Équation du mouvement d'un pendule simple

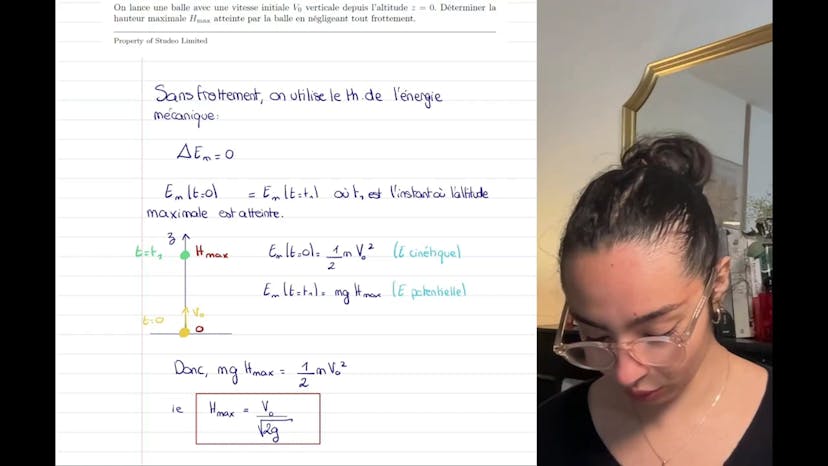
Aujourd'hui, nous allons établir l'équation du mouvement du pendule simple en utilisant les théorèmes énergétiques. Un pendule simple est un point matériel accroché à l'extrémité d'un fil tendu. Nous souhaitons exprimer l'énergie mécanique de ce pendule et justifier pourquoi elle est constante. L'énergie mécanique est composée de l'énergie potentielle (Ep) et de l'énergie cinétique (Ec). Nous pouvons l'écrire comme Ep = mgh + 1,5mv², où m est la masse, g est l'accélération due à la pesanteur, h est la hauteur de la bille et v est sa vitesse. La hauteur h du pendule peut être exprimée comme h = l - lcosθ, où l est la longueur du fil et θ est l'angle que fait le pendule par rapport à la verticale. En utilisant cette expression de la hauteur, nous pouvons retrouver l'énergie potentielle de pesanteur : Ep = mgl(1 - cosθ). Maintenant, nous avons une expression de l'énergie mécanique complète, mais nous devons également prendre en compte l'énergie cinétique. En utilisant les coordonnées polaires, nous pouvons exprimer le vecteur vitesse de la bille (om) comme om = lθ. En dérivant ce vecteur par rapport au temps, nous obtenons l'accélération angulaire : dθ/dt = θ'. La vitesse de la bille peut donc être écrite comme Ec = 1/2ml²(θ')². Ainsi, l'énergie mécanique totale (em) s'écrit em = mgl(1 - cosθ) + 1/2ml²(θ')². Maintenant, nous devons montrer que cette énergie est constante. Dans le cas d'un mouvement conservatif, sans frottement, nous avons em = constante. En dérivant em par rapport au temps, nous obtenons dem/dt = mglθsinθ + 1/2ml²θ'². Pour que dem/dt soit égal à zéro (pour avoir une grandeur constante), nous devons avoir gsinθ + lθ'² = 0. Cette équation est l'équation du pendule simple. Bien que cette méthode ne soit pas nécessairement plus rapide que le principe fondamental de la dynamique, elle permet d'utiliser une approche énergétique différente qui peut être plus simple dans certains cas. J'espère que cela vous a été utile. N'hésitez pas à poser vos questions dans les commentaires.