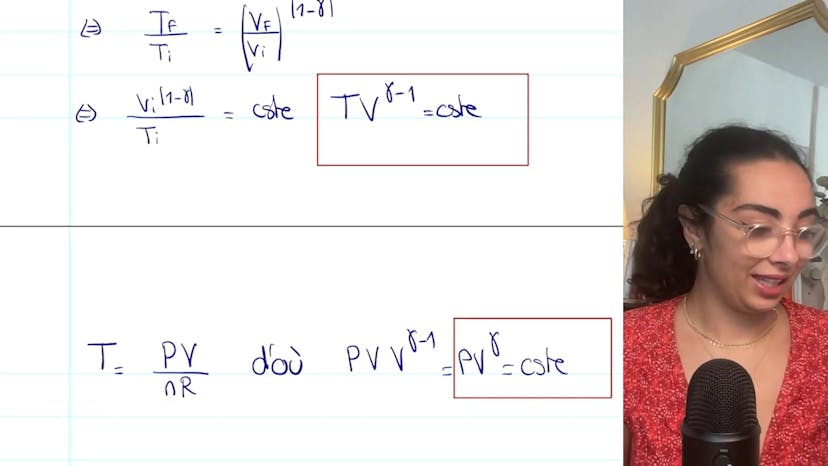Gaz dans une enceinte

Bonjour à tous ! Aujourd'hui, nous allons étudier un exercice sur le second principe de la thermodynamique concernant un gaz dans une enceinte. Dans cet exercice, nous avons une enceinte indéformable avec des parois calorifugées, séparée en deux compartiments par une cloison d'air étanche, diatherme et mobile. Chaque compartiment contient le même gaz parfait. Au départ, le gaz du premier compartiment est à une température T0, une pression P0 et un volume V0, tandis que celui du deuxième compartiment a une pression deux fois plus grande, soit 2P0, avec les mêmes température T0 et volume V0. On laisse ensuite la cloison bouger librement jusqu'à atteindre l'équilibre. Pour déterminer l'état final, nous utilisons le premier principe de la thermodynamique. Comme l'enceinte est indéformable et calorifugée, la variation d'énergie interne est nulle. Nous avons donc Tf = T0, la température ne change pas. En utilisant la loi des gaz parfaits, nous calculons les pressions finales des compartiments : P1 = nRT0/V1 et P2 = nRT0/V2, avec V1 et V2 étant respectivement les volumes finaux des compartiments. Nous utilisons ensuite les deux équations de conservation du volume total de l'enceinte (2V0) et de la relation entre V1 et V2 (V2 = 2V1) pour trouver les valeurs des volumes V1 et V2. Finalement, en insérant ces valeurs dans les équations de pression, nous obtenons la pression finale P = 3n0RT0/2V0. Pour calculer la variation d'entropie, nous utilisons la formule ΔS = nCVM ln(TF/TI) + nR ln(VF/VI). Comme la transformation est isotherme, nous avons TF = TI. Ainsi, la variation d'entropie devient ΔS = nR ln(V1/V0) + 2n0R ln(V2/V0). En utilisant les valeurs des volumes déterminées précédemment, nous trouvons ΔS = n0R ln(32/27), qui est positif puisque 32 est supérieur à 27. En conclusion, pour déterminer l'état final, nous utilisons le premier principe et les lois des gaz parfaits. Pour calculer la variation d'entropie, nous utilisons le second principe et les formules de variation d'entropie.