Régime sinusoïdal forcé

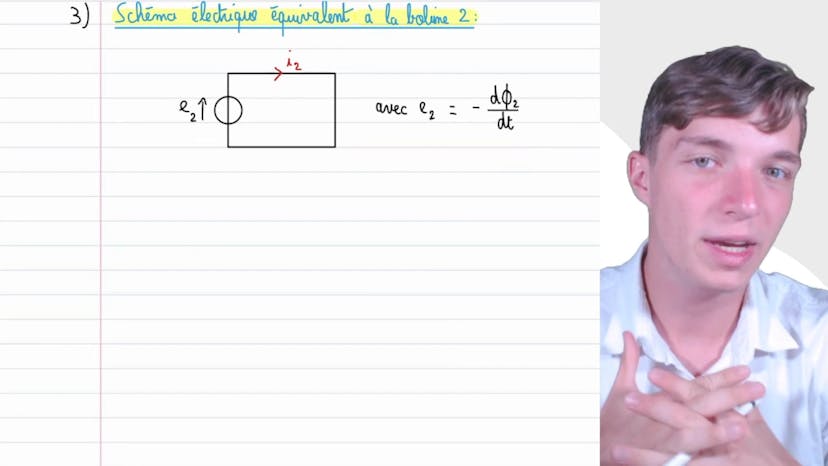
Dans cette vidéo, on étudie une bobine dans le cadre du régime sinusoïdal forcé. On cherche à montrer que l'inductance L de la bobine est égale à mu0 N² divisé par A fois S. Pour cela, on calcule le flux propre du champ magnétique généré par la bobine, qui est égal à Mu0 N² S divisé par A. Ensuite, on ajoute un champ magnétique extérieur Bext qui est égal à B0 sinus oméga T fois EZ. On détermine la force électromotrice d'induction en prenant en compte à la fois le flux propre et le flux du champ magnétique extérieur. On obtient une équation différentielle vérifiée par le courant I, qui est d2I sur dt plus I divisé par tau est égal à moins EM sur L cosinus oméga T. On détermine l'expression de EM et de tau à partir de cette équation. Les solutions de cette équation sont cherchées sous la forme d'un courant I de T égal à IM cosinus oméga T plus Psi. On utilise la notation complexe pour déterminer l'amplitude complexe IM en fonction de EM, oméga, L et tau. On obtient IM complexe égal à moins EM tau divisé par L facteur de 1 plus J oméga tau. On détermine ensuite l'amplitude IM réelle et la phase Psi en utilisant les propriétés de l'argument d'un nombre complexe. Enfin, on analyse les valeurs obtenues sans l'auto-induction et on constate que son apport est négligeable par rapport au champ magnétique extérieur. Cet exercice complexe demande de bonnes compétences en manipulation et conceptualisation de la bobine.