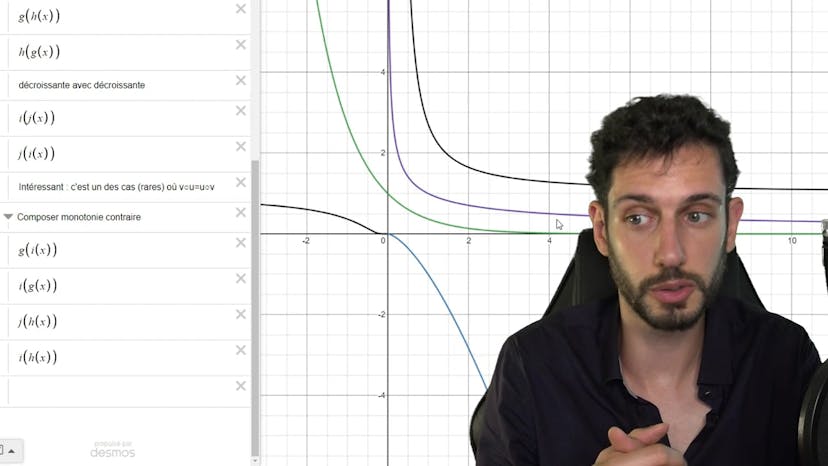
Fonction Composée

Dans ce cours, on apprend à étudier une fonction composée, en utilisant l'exemple de la fonction e^(2x-1)/x^2. On explique que la fonction est de la forme h-g^2x, où g est -1/x^2 et h est e^(2x-1), et qu'il est important de bien comprendre ces deux fonctions pour étudier leur composition. On utilise ensuite les formules de dérivation pour trouver le sens de variation de g et son tableau de variation, ainsi que les limites de la fonction aux bornes. Ensuite, on calcule le sens de variation de f (g-h), en appliquant les règles de variation (croissant composé avec croissant fait croissant, décroissant composé avec décroissant fait croissant, etc.) On trouve finalement que la fonction est décroissante sur R* et croissante sur R*+, avec des limites en moins l'infini et plus l'infini de 1, et une limite en 0 de 0 (qui peut être prolongée par continuité). On explique que cela peut être fait en calculant la dérivée de la fonction, ou en étudiant directement la fonction composée.