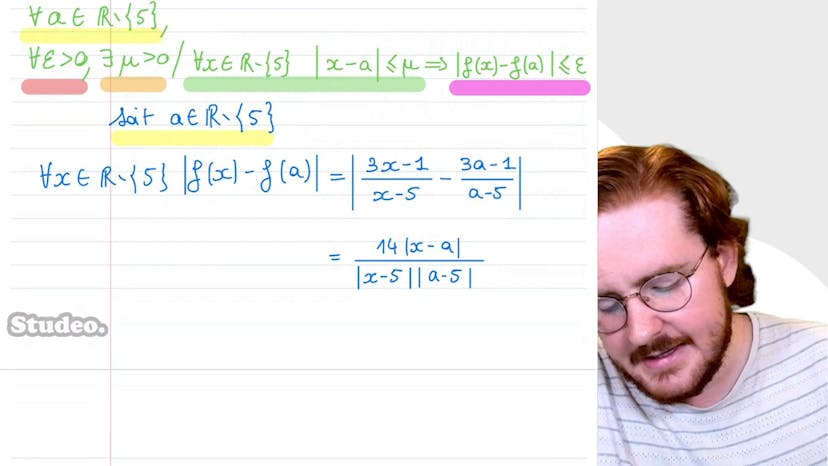
Détermination d'une limite à l'aide de la définition formelle

Bonjour, je suis Paul et je vais résumer ce cours en utilisant des techniques d'optimisation pour le référencement naturel (SEO). Dans cette vidéo, nous abordons un exercice complexe sur les continuités et les limites. L'énoncé est le suivant : si f(x+1) - f(x) converge vers une limite réelle L lorsque x tend vers l'infini, nous devons montrer que f(x)/x a également la même limite L. Pour résoudre cet exercice, nous commençons par écrire f(x+1) - f(x) convergent vers L. En manipulant cette inégalité, nous obtenons f(x)/x avec des termes qui tendent vers 0. Cependant, nous ne pouvons pas directement utiliser ces informations pour prouver notre résultat. L'idée clé est de sommer cette inégalité sur un n choisi judicieusement, puis de contrôler ces termes pour éviter qu'ils tendent vers 0. Nous utilisons la continuité de f à un certain moment pour borner la fonction et l'écraser avec x tendant vers 0. En résumé, nous démontrons que f(x)/x converge vers L en utilisant des encadrements pour contrôler les termes qui tendent vers 0 et en jouant sur la continuité de f pour borner la fonction. J'espère que vous avez bien suivi. N'hésitez pas à revoir l'exercice si vous avez des questions. À la prochaine fois !