Association de dipôles

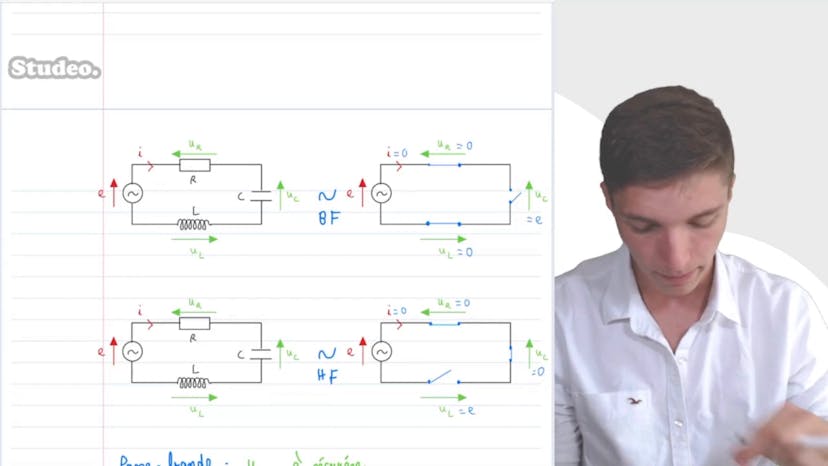
Dans cette vidéo, Mathilde Studio explique comment associer des dipôles de manière complexe. Elle commence par montrer un bout de circuit composé d'une résistance et d'un condensateur en série. Elle explique ensuite comment déterminer l'impédance équivalente aux dipôles en régime sinusoidal, ainsi que sa résistance et sa réactance. Elle souligne que l'impédance équivalente permet d'identifier des dipôles à des résistances, tout comme les associations de résistances. Elle montre comment l'impédance des dipôles en série s'ajoutent pour donner la somme des impédances. Elle déduit la nature des dipôles ainsi formés, qui comportent une partie résistive et une partie capacitive. Elle explique comment relier la tension complexe E qui s'applique à l'ensemble des dipôles au courant complexe I qui les traverse, et comment obtenir des signaux en quadrature de phase. Elle détermine finalement l'expression réelle de E pour I², qui vaut I0 sin ωt, en appliquant la loi d'Ohm en complexe et en utilisant une manipulation qui consiste à passer du signal complexe au signal réel en intégrant ou en dérivant. Elle insiste sur l'importance de cette transformation en complexe pour simplifier les calculs.