Filtre passe-haut RLC

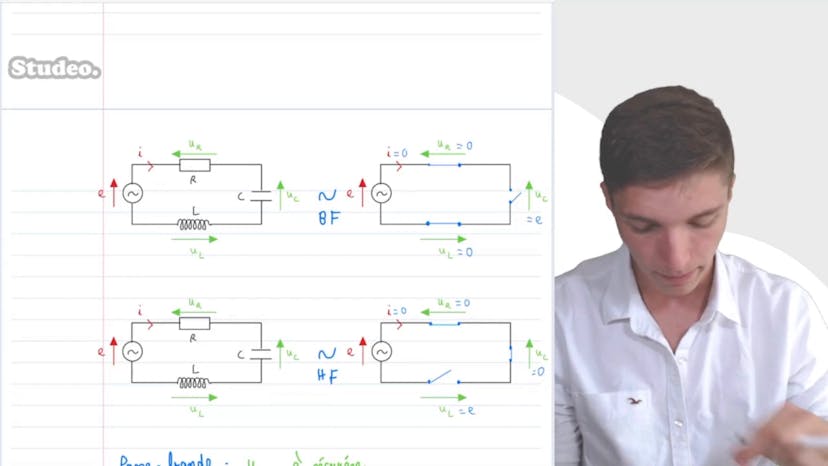
Bonjour à tous, dans cette vidéo, nous allons réaliser un filtre passe-eau pour un circuit RLC série. Pour cela, nous devons justifier que ce filtre est bien passe-eau, définir sa pulsation caractéristique ω0 et son facteur de qualité Q. Pour déterminer le caractère passe-eau du circuit, nous devons mener une étude asymptotique. Dans une précédente vidéo, nous avons démontré que le circuit RLC série est équivalent à un circuit basse fréquence et un circuit haute fréquence. Ainsi, pour réaliser un filtre passe-eau, nous devons sélectionner la tension aux bornes de la bobine, car elle filtre les basses fréquences. La pulsation propre et le facteur de qualité du filtre peuvent être déterminés en utilisant la méthode classique pour un circuit RLC série. Nous devons ensuite exprimer la fonction de transfert du filtre sous la forme h = jqx / (1 + jqx - 1/x). Pour cela, nous utilisons le diviseur de tension avec les impédances complexes. En normalisant la fonction de transfert, nous obtenons l'équation demandée. Ensuite, nous devons déterminer les pentes des asymptotes du diagramme de Bode-Anguin, en supposant que le facteur de qualité du circuit n'est pas raisonnable. Pour calculer le module de la fonction de transfert, nous utilisons l'expression qx / (1 + q²x² - 1/x²) et déterminons le terme dominant en basse fréquence et en haute fréquence. En basse fréquence, la pente est de 40 décibels par décade et en haute fréquence, la pente est de 0. En traçant le diagramme de Bode en fonction du logarithme de la pulsation, nous pouvons esquisser l'allure du filtre passe-eau. Enfin, nous étudions si le filtre peut avoir un comportement dérivateur ou intégrateur. Cela se remarque sur le diagramme de Bode par une pente de plus ou moins 20 décibels par décade. Dans ce cas, le filtre n'a pas de comportement dérivateur ou intégrateur. Le diagramme de Bode est donc un outil très utile pour visualiser rapidement les caractéristiques d'un filtre. Merci pour cette étude du filtre passe-eau d'un RLC et à bientôt.