La Guerre des étoiles

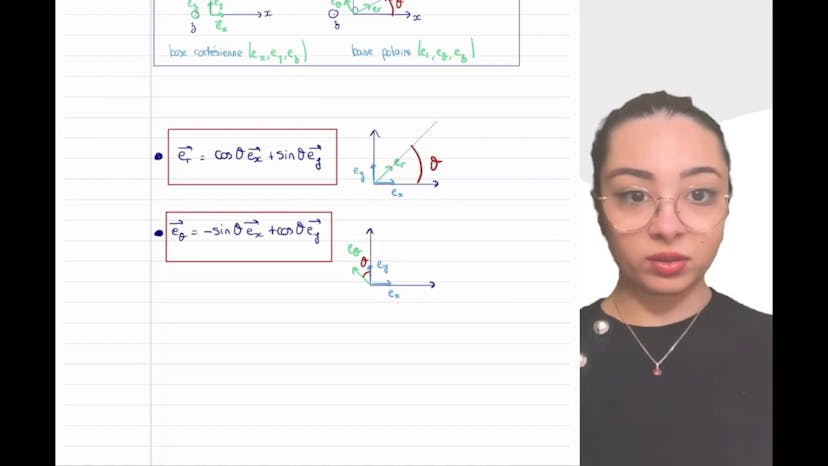
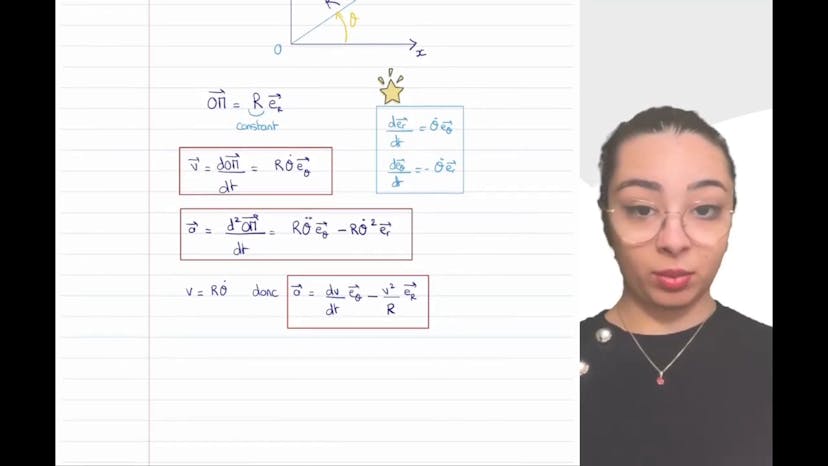
Dans cet exercice de physique sur la cinématique, un véhicule suit une trajectoire sinusoidale entre des cheminées d'une usine. La vitesse du véhicule est constante selon x et il met 12 secondes pour revenir sur l'axe après la sixième cheminée. L'amplitude de la sinusoïde doit être déterminée pour que l'accélération reste inférieure à 10G en valeur absolue. Pour modéliser le mouvement sinusoidal, l'utilisation d'un sinus ou d'un cosinus est avantageuse en fonction du point de départ. La période du sinus est de 2 pi et la hauteur est donnée par la formule Y0 sinus de pi X sur L. En isolant le temps dans l'équation de trajectoire et en dérivant une fois et deux fois, l'accélération selon y peut être calculée. Pour limiter l'accélération en dessous de 10G, l'amplitude de la sinusoïde doit être inférieure à 40 mètres. L'exercice montre également comment convertir les mètres par seconde en kilomètres par heure.