Cours de Limite et continuité en Ligne par les Meilleurs Professeurs - Limite et continuité

Continuité en un point

Dans cette vidéo, Paul nous parle de la continuité de la fonction g définie sur R. La fonction g est définie comme suit : - g(x) = 1/|x| si x n'est pas égal à -1, 0 ou 1 - g(x) = 0 si x est égal à -1, 0 ou 1 Tout d'abord, on étudie la continuité de g sur R privé de -1, 0 et 1. On remarque que g ne s'annule pas sur R privé de -1, 0 et 1, donc la fonction x1 sur le diagramme de valeur absolue de x est continue sur -1, 0 et 1. Donc, g est continue sur R privé de -1, 0 et 1. Ensuite, on étudie la continuité de g en -1, 0 et 1. Pour cela, on calcule les limites de g lorsque x tend vers -1, 0 et 1. La limite de g(x) quand x tend vers 0 avec x différent de 0 est égale à la limite de 1/|x| quand x tend vers 0, et cette limite est égale à 0, qui est la valeur de g(0). Donc, g est continue en 0. Par contre, la limite de g(x) quand x tend vers 1 avec x différent de 1 est égale à la limite de 1/|x| quand x tend vers 1, et cette limite est égale à l'infini. Donc, g n'est pas continue en 1. De la même manière, g n'est pas continue en -1, car la limite de g(x) quand x tend vers -1 avec x différent de -1 est également infinie. Ainsi, on conclut que g est continue sur R privé de -1 et 1. C'est la fin de cet exercice, à bientôt pour une prochaine vidéo !

Continuité avec paramètres

Dans cette vidéo, Paul explique la continuité des fonctions. Il commence par étudier la continuité de la fonction f pour une valeur a donnée. Il décompose la fonction en plusieurs morceaux continus et vérifie qu'ils se raccordent correctement. Il conclut que la fonction f est continue si et seulement si a est égal à 0 ou 1. Ensuite, Paul examine la fonction g et cherche les valeurs des constantes α, β et γ pour lesquelles la fonction est continue. Il analyse les points de raccordement et utilise des équations pour déterminer les relations entre les constantes. Il trouve que f est continue si α + β = 1 et γ + β = 1. Il en déduit que α = γ et que β = 1 - γ. Ainsi, f est continue pour α, β, γ appartenant à l'ensemble (x, 1-x, x) pour x appartenant à R, où γ est libre et peut prendre n'importe quelle valeur réelle. En résumé, la vidéo explique les concepts de continuité des fonctions, examine la continuité de la fonction f pour différentes valeurs a, et détermine les valeurs des constantes α, β, γ pour lesquelles la fonction g est continue.

Prolongements par continuité de fonctions cosinus et sinus

Dans cette vidéo, nous étudions le prolongement par continuité de fonctions contenant des sinus et des cosinus. Nous commençons par examiner la fonction f2x = sin(x) * sin(1/x), qui n'est pas définie en 0 et -1. Nous constatons que sin(1/x) n'a pas de limite en 0, mais sin(x) est borné. Ainsi, f est continue sur l'intervalle réel positif, et f peut être prolongée par continuité en 0 en définissant f(x) = 0. Ensuite, nous examinons la fonction g(x) = cos(x) * cos(1/x). Nous avons déjà vu que cos(1/x) n'a pas de limite en 0, et en démontrant que les limites de deux suites u et v, qui tendent toutes deux vers 0, sont différentes lorsque nous les appliquons à g, nous concluons que g n'a pas de limite en 0. Par conséquent, g ne peut pas être prolongée par continuité en 0. Finalement, nous étudions la fonction h(x) = sin(x+1) * ln|1+x|. Nous examinons la limite de h(x) lorsque x tend vers -1 et constatons qu'elle est indéterminée. Pour résoudre cette indétermination, nous utilisons l'astuce de poser u = x+1, ce qui nous permet de réécrire h(x) en termes de sin(u) et ln|u|. Nous utilisons ensuite les connaissances sur les limites du sinus et du logarithme en 0 pour déterminer la limite de h(x) lorsque x tend vers -1. En utilisant la croissance comparée, nous concluons que la limite de h(x) est égale à 0. Par conséquent, h peut être prolongée par continuité sur l'ensemble des réels en définissant h(x) = 0 lorsque x = -1. Ceci conclut l'exercice sur les prolongements par continuité des fonctions avec des sinus et des cosinus à l'intérieur.

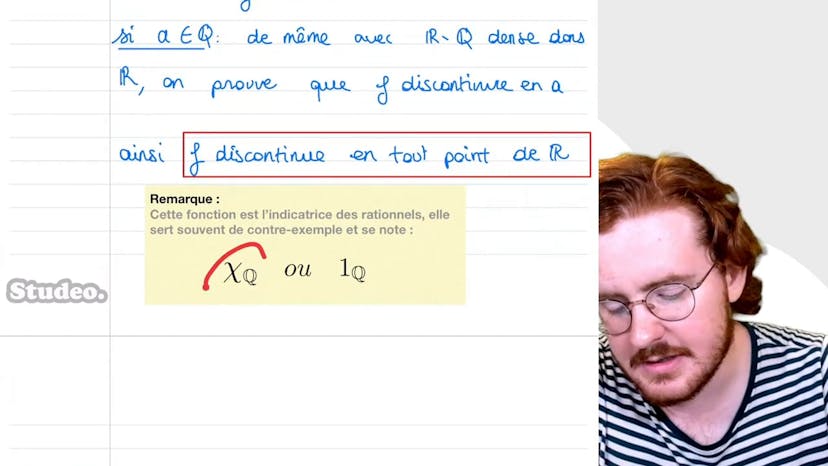
Indicatrice de Q

Dans ce cours, Paul aborde la fonction f de R dans R, qui est définie comme suit : f(x) = 1 si x est rationnel, et f(x) = 0 si x n'est pas rationnel. Cette fonction est appelée la fonction indicatrice des rationnels. Pour démontrer que f est discontinue en tout point, Paul explique qu'il suffit de visualiser la fonction. Comme les rationnels sont présents partout dans R, on peut imaginer deux droites qui se croisent en chaque point. Cependant, les points sont si proches les uns des autres qu'ils semblent alignés, donnant une impression de continuité. Cependant, la fonction alterne constamment entre 0 et 1 à chaque changement de rationnel à irrationnel, ce qui montre qu'elle n'est pas continue. Paul montre ensuite comment prouver la discontinuité de f en utilisant la caractérisation séquentielle de la continuité. Il explique qu'il suffit de trouver une suite de réels qui converge vers un point a donné, mais dont les images par f ne convergent pas vers f(a). En utilisant la densité de Q (les rationnels) dans R, Paul démontre que f est discontinue en a, que a soit un rationnel ou un irrationnel. Il conclut en précisant que cette fonction, qui est simple mais discontinue en tout point, est souvent utilisée comme un contre-exemple dans l'étude de la continuité. Elle est notée qui-q ou un-q, et est appelée l'indicatrice des irrationnels. C'est ainsi que se termine ce cours, avec une invitation à la prochaine fois.

Fonctions min et max

Dans cette vidéo, Paul explique comment prouver que les fonctions minimum et maximum de deux autres fonctions, f et g, sont également continues. Il commence par souligner qu'il existe différentes méthodes pour prouver la continuité d'une fonction, comme la définition traditionnelle ou l'utilisation de suites. Cependant, il affirme que la façon la plus rapide est d'utiliser des théorèmes généraux. Paul rappelle également qu'il est possible d'exprimer les fonctions minimum et maximum en fonction de f et g à l'aide de fonctions visuelles qui sont déjà connues pour être continues. Pas besoin de les redémontrer. Il explique ensuite comment exprimer le minimum et le maximum en termes de valeurs a et b dans R². Il fait remarquer que la somme du maximum et du minimum de a et b est égale à a + b. Ensuite, il explique qu'en utilisant la somme et la différence, on peut obtenir une expression pour le minimum et le maximum en utilisant demi-somme et demi-différence. Il note que le maximum de a et b et le minimum de a et b sont égaux à la distance entre a et b, qui est équivalente à la valeur absolue de a - b. Ainsi, il conclut que le maximum de f et g est égal à la somme de f et g, plus la valeur absolue de f - g, le tout divisé par 2. Et le minimum de f et g est égal à la somme de f et g, moins la valeur absolue de f - g, également divisé par 2. En utilisant ces expressions et les théorèmes généraux, il montre que les fonctions minimum et maximum de f et g sont continues en x0. Paul insiste sur l'importance de prendre du recul dans cet exercice et de ne pas se précipiter dans des démonstrations complexes. Il souligne qu'il faut réfléchir à l'astuce et aux connaissances sur les fonctions minimum et maximum. Faire un dessin peut également aider à visualiser les concepts. En conclusion, Paul affirme que les fonctions minimum et maximum de f et g sont continues en x0, et il encourage les spectateurs à réfléchir davantage avant de se lancer dans des démonstrations complexes.