Cours de Electrocinétique en Ligne par les Meilleurs Professeurs - Electrocinétique

RC série

Dans cette vidéo, Matisse de Studio étudie le circuit RC série. Le circuit est composé d'un générateur de tension continue, d'une résistance et d'un condensateur. L'objectif est d'établir l'équation différentielle vérifiée par la tension au bord du condensateur (UC). Pour cela, Matisse utilise la loi des mailles qui indique que UC + RI = E. Il remplace ensuite le courant (I) par C * dUC/dt, où C est la capacité du condensateur. En simplifiant l'expression, il obtient l'équation différentielle : dUC/dt + (1/RC) * UC = E/(RC). Pour résoudre cette équation, Matisse détermine les conditions initiales. Le condensateur est initialement déchargé, ce qui signifie que UC(0-) = 0. Il utilise ensuite cette condition de continuité pour déterminer la constante dans la solution générale de l'équation homogène. Ensuite, Matisse cherche une solution particulière en supposant que la tension est constante par rapport au temps. Il trouve que la tension associée est E. En sommant la solution générale et la solution particulière, il obtient la solution globale de l'équation différentielle : UC(t) = E * (1 - exp(-t/RC)). Matisse représente graphiquement cette solution, montrant qu'elle augmente exponentiellement et tend vers E lorsque t tend vers l'infini. Il calcule également la dérivée de UC par rapport au temps en t = 0, qui vaut E/(RC). Enfin, Matisse effectue une étude énergétique du circuit. Il montre que l'énergie accumulée dans le condensateur au cours de l'évolution du régime vaut 1.5 * C * E^2. De plus, l'énergie dissipée par l'effet joule dans la résistance est également de 1.5 * C * E^2. Ainsi, la somme de l'énergie accumulée et dissipée égale l'énergie fournie par le générateur. En conclusion, cette vidéo donne une étude complète du circuit RC série, en expliquant les étapes pour établir l'équation différentielle, résoudre celle-ci et effectuer une étude énergétique.

RL série

Dans cette vidéo, Matisse de Studio étudie le circuit RL série en analysant la décharge d'une bobine lorsque l'interrupteur est ouvert en régime permanent. En établissant l'équation différentielle, on résoud l'équation et détermine l'intensité à travers la bobine. La représentation de la solution montre une exponentielle décroissante, avec une tangente négative et un temps caractéristique pour atteindre 0,63% de la valeur finale. L'étude énergétique montre que l'énergie stockée dans la bobine est dissipée par effet Joule, permettant ainsi de redémontrer que l'énergie de la bobine se perd par cette dissipation.

Bobines et resistances

Dans cette vidéo, Matisse de Studio explique comment déterminer l'équation différentielle liant la tension et le courant d'un circuit constitué de deux branches en parallèle, avec une bobine et une résistance en série dans chaque branche. Pour résoudre cette question, on peut utiliser les différentes relations entre la tension et les courants dans chaque branche, ainsi que la loi des nœuds en Ré. En manipulant ces équations avec des dérivées et des combinaisons, on peut exprimer I en fonction de U et obtenir l'équation différentielle recherchée. Malgré son caractère calculatoire, cet exercice montre l'importance de se concentrer sur les grandeurs que l'on cherche à démontrer et de manipuler les expressions pour les faire apparaître.

Circuit alimenté par deux générateurs

Bonjour à tous, dans cette vidéo, nous étudions un circuit alimenté par deux générateurs. Le circuit est composé d'un générateur de tension continue E en série avec une résistance R, et d'un autre générateur de tension E/2 en série avec une résistance R/2. Pour établir les équations différentielles, nous utilisons la loi des mailles pour chaque maille du circuit. On obtient ainsi deux relations : UC(t) = (E/2)*R*I1(t) et UC(t) + R*I2(t) = 2. En utilisant la loi des noeuds, nous obtenons une relation entre le courant I(t) traversant le condensateur, I1(t) et I2(t). En combinant toutes ces relations, nous obtenons une équation différentielle : (d^2UC/dt^2) + (3/(RC))*dUC/dt = (2/(RC))*E. Nous résolvons ensuite cette équation différentielle en trouvant la solution générale associée à l'équation homogène, puis en cherchant une solution particulière. En combinant ces solutions, nous obtenons l'expression complète de UC(t) : UC(t) = (E/3)*(2 + e^(-3t/RC)). Nous déterminons également les constantes de l'équation en utilisant les conditions initiales. Pour cela, nous utilisons le fait que le courant I2(t) était nul avant la fermeture de l'interrupteur, ce qui implique que UC(t=0-) = UC(t=0+) = E. En utilisant ces conditions, nous trouvons que UC(t=0) = E/3. Ensuite, nous déterminons le temps T1 nécessaire pour que UC(t) atteigne sa valeur finale à 1% près. Grâce à l'expression de UC(t), nous remplaçons UC(t) par sa valeur atteinte à 99% de sa valeur finale, ce qui nous permet d'isoler T1 dans l'expression. Nous trouvons ainsi que T1 = -(RC)*ln(0.02/3). Enfin, nous exprimons la puissance dissipée par effet Joule dans le circuit. En utilisant la loi d'Ohm, nous exprimons les tensions aux bornes des résistances en fonction de UC(t) et E. En remplaçant UC(t) par son expression, nous obtenons l'expression de la puissance dissipée. Nous remarquons que cette puissance tend vers E^2/(6R) lorsque t tend vers l'infini, ce qui est cohérent avec un raisonnement physique basé sur l'analyse du circuit. En résumé, cette vidéo présente l'étude d'un circuit alimenté par deux générateurs. Nous établissons les équations différentielles et résolvons l'équation pour trouver l'expression de la tension aux bornes du condensateur. Nous déterminons également le temps nécessaire pour atteindre la valeur finale de la tension, et exprimons la puissance dissipée par effet Joule dans le circuit.

Circuit RC parallèle

Dans cette vidéo, Matisse de Studio étudie un circuit RC en parallèle, dans lequel l'interrupteur K est brusquement fermé. Pour trouver l'expression de la tension U et tracer son allure, il applique la loi des mailles et normalise l'équation différentielle pour obtenir une solution générale et particulière. Il détermine une condition initiale à partir du régime permanent précédent et utilise cette information pour déterminer la constante arbitraire de sa solution. Enfin, il trace l'allure de la tension U en utilisant les informations trouvées précédemment et conclut que le condensateur ne se décharge pas totalement, restant à une tension de E sur 2.

Circuit RL à deux mailles

Dans cette vidéo, Matisse de Studio étudie un circuit RL à 2 mailles. Il faut étudier l'évolution de la tension S aux bornes d'un dipôle en dérivation composé d'une résistance R sur 2 et d'une bobine L. Le circuit est alimenté par un générateur de tension continue E en série avec une résistance R. Pour résoudre le circuit, la méthode classique de résolution est utilisée, en établissant l'équation différentielle et en trouvant la solution générale ainsi que la solution particulière. Les conditions initiales sont obtenues en appliquant la continuité du courant à travers la bobine. La solution de l'équation est S de t est égal à E sur 3 exponentielle de moins R sur 3 L fois t. Des informations supplémentaires sont données pour tracer la courbe de la tension.

Décharge de deux condensateurs

Dans cette vidéo, Matisse de Studio étudie la décharge de deux condensateurs en série. Il résout une équation différentielle en utilisant la loi des mailles et la relation courant-tension du condensateur. Il détermine également la variation d'énergie du système constitué par la résistance et les condensateurs. Il démontre que l'énergie dissipée par effet Joule dans la résistance est égale à la valeur absolue de la variation d'énergie du système total. Enfin, il explique comment ce phénomène décrit concrètement ce qui se passe à l'intérieur d'un système électrique.

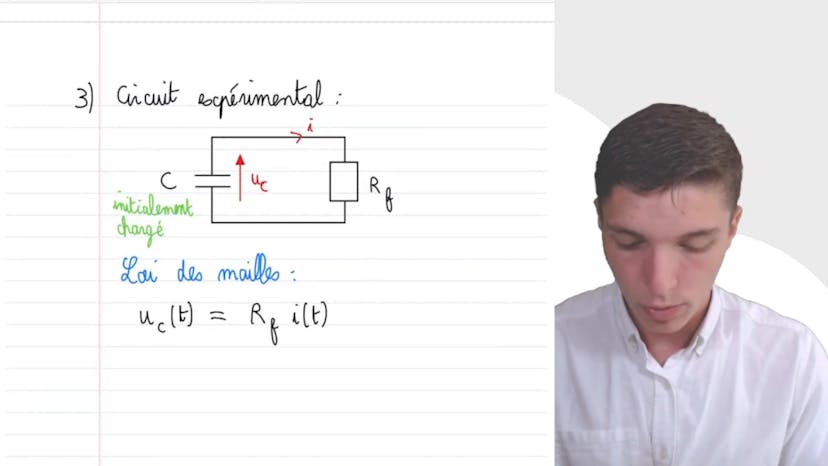
Résistance de fuite

Dans cette vidéo, on étudie la modélisation d'une résistance de fuite d'un condensateur après avoir observé expérimentalement la décharge spontanée d'un condensateur de capacité 100 pF initialement chargé sous une tension de 10V. On explique que cette décharge est causée par le phénomène de fuite, où les électrons qui se trouvent sur une des plaques du condensateur peuvent passer à travers l'isolant qui sépare les deux plaques. On modélise ce phénomène en ajoutant une résistance en parallèle avec le condensateur. Pour calculer l'ordre de grandeur de la résistance de fuite, on propose un circuit comprenant un condensateur initialement chargé et une résistance de fuite en série, et on pose une équation différentielle pour la tension du condensateur en régime permanent. En résolvant cette équation différentielle et en utilisant les données expérimentales, on isole la résistance de fuite, qui est finalement égale à 0.5 MHz. Cette résistance est très importante car elle permet au condensateur de retenir les charges passées.