 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Divisibilité et division euclidienne
- Congruences
- PGCD et algorithme d’Euclide
- Nombres premiers
- Prépare tes écrits
- Loi usuelles, groupes
- Anneaux corps
- 11- Prépare tes écrits
- Opérations sur les matrices
- Puissance de matrices
- Systèmes linéaires et Inverses de matrices
- 12- Prépare tes écrits
- Espaces vectoriels et sous-espaces vectoriels
- Famille de vecteurs
- Somme d'espaces vectoriels
- Matrices applications linéaires
- Changement de base, matrices de passages
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Divisibilité et division euclidienne
- Congruences
- PGCD et algorithme d’Euclide
- Nombres premiers
- Prépare tes écrits
- Loi usuelles, groupes
- Anneaux corps
- 11- Prépare tes écrits
- Opérations sur les matrices
- Puissance de matrices
- Systèmes linéaires et Inverses de matrices
- 12- Prépare tes écrits
- Espaces vectoriels et sous-espaces vectoriels
- Famille de vecteurs
- Somme d'espaces vectoriels
- Matrices applications linéaires
- Changement de base, matrices de passages
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Algèbre
MPSI/PCSI

Famille libre
Ce cours traite de la notion de liberté ou de liaison d'une famille de vecteurs. L'objectif est de déterminer si une famille donnée est libre ou liée en utilisant une méthode classique. On suppose l'existence d'une combinaison linéaire qui lie tous les éléments de la famille ensemble, et on cherche à trouver une contradiction à cette hypothèse. Si une telle combinaison linéaire existe, alors tous les coefficients doivent nécessairement être égaux à zéro, ce qui prouve que la famille est libre.
On écrit donc cette combinaison linéaire et on la traduit en un système d'équations, qu'on résout pour trouver les coefficients lambda et mu. Si on trouve que tous les coefficients sont nuls, cela signifie que la famille est libre. On répète cette démarche pour différentes paires de vecteurs de la famille pour déterminer si elles sont libres ou liées.
Enfin, pour déterminer si la famille de vecteurs dans son ensemble est libre ou liée, on rédige une nouvelle combinaison linéaire en introduisant des coefficients lambda1, lambda2, et lambda3, et on cherche à trouver si cette combinaison linéaire a une solution unique. Si elle en a, alors la famille est liée, sinon elle est libre.
Dans l'exemple donné, on observe que la famille v1, v2, v3 est liée, car il est possible de trouver une combinaison linéaire telle que -2v1 + v2 - v3 = 0, ce qui montre que les trois vecteurs sont liés dans un plan et qu'aucun d'entre eux ne sort de ce plan. Cela signifie que la famille ne couvre pas l'ensemble de l'espace, ce qui fait qu'elle est liée.
Maths
Algèbre
MPSI/PCSI

Famille liée
Le cours traite des familles libres et de leur complexité croissante dans les exercices proposés. Le thème de l'exercice est l'espace vectoriel et les suites réelles. Trois suites différentes sont considérées : la suite des cosinus nθ, la suite cosinus nθ plus a, et la suite cosinus nθ plus b. Le but est de déterminer si la famille est liée.
L'approche utilisée est d'appliquer la formule trigo cos(a + b) = cos(a) cos(b) - sin(a) sin(b) aux deux suites complexes. En utilisant cette formule, on peut réécrire les deux suites en termes de cos(nθ) et quelques coefficients réels. Cependant, il reste un terme contenant sin(nθ) qui dépend de n et rend la famille difficile à combiner.
Pour éliminer ce terme, l'idée est d'utiliser une combinaison des suites en multipliant la première par sin(b) et la deuxième par sin(a), puis en soustrayant les deux résultats. Cela permet d'obtenir une expression ne contenant plus le terme problématique. En reconnaissant une autre formule trigo, on peut écrire une combinaison linéaire des éléments de la famille : cos(nθ) = cos(a) sin(b) - cos(b) sin(a).
Cette combinaison linéaire prouve que la famille est liée. L'exercice illustre ainsi la complexité croissante des tests de liberté et la nécessité de développer des compétences pour les résoudre. Le professeur conclut en invitant les étudiants à poser des questions et en promettant une prochaine vidéo.
Maths
Algèbre
MPSI/PCSI
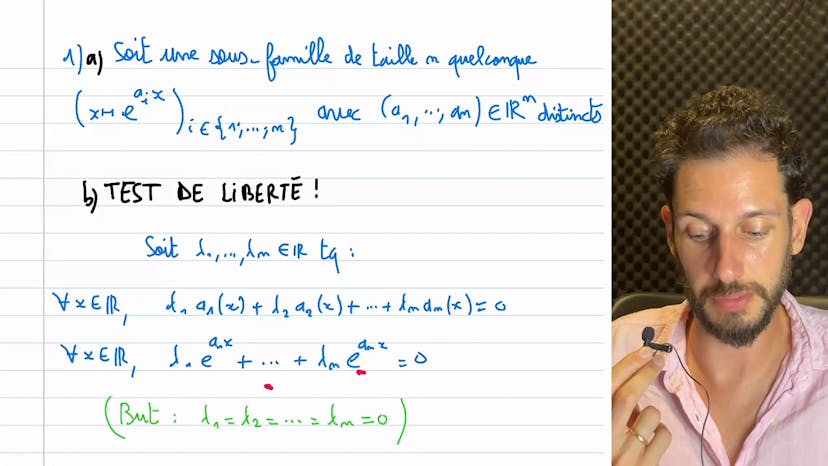
Liberté et familles de fonctions
Aucun résumé n'est disponible pour cette vidéo
Maths
Algèbre
MPSI/PCSI
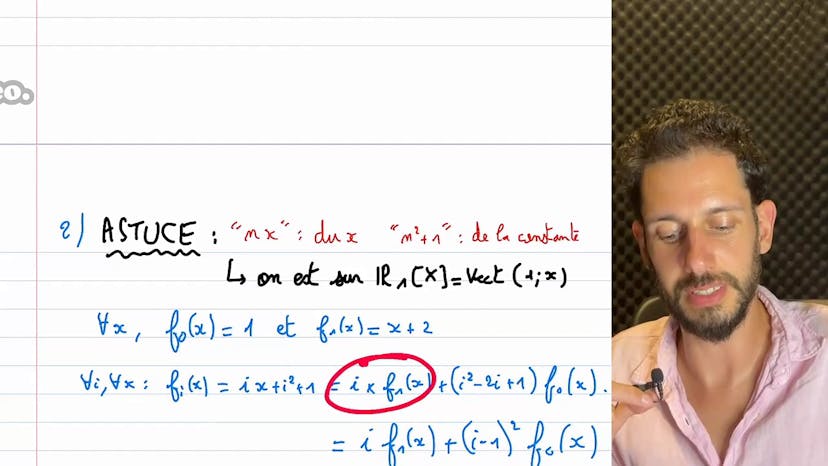
Encore des familles de fonctions
Le cours porte sur la question de savoir si une famille de fonctions est libre ou non. Dans la question 1, on nous donne trois fonctions sinus différentes et on nous demande de montrer si elles sont liées. Tout d'abord, on utilise quelques formules trigonométriques pour exprimer ces fonctions uniquement en fonction de sinus. Ensuite, on montre que deux des fonctions sont liées à sinus x et on fait la même démarche avec la troisième fonction pour obtenir une relation entre les trois fonctions. Ainsi, on conclut que la famille est liée.
Dans la question 2, on nous donne une famille de fonctions qui sont des polynômes de degré 1. Au début, l'auteur se perd un peu dans ses calculs, mais réalise finalement que toutes ces fonctions sont en fait des combinaisons linéaires d'une constante et de x. Donc, quel que soit l'élément de la famille, on peut l'exprimer comme une combinaison linéaire des deux premiers éléments de la famille. Donc, toute sous-famille de cette famille est également liée, ce qui signifie que la famille entière est liée.
En conclusion, le cours traite de la question de la liberté d'une famille de fonctions. Dans les deux questions abordées, on montre que les familles sont liées, ce qui signifie qu'elles ne sont pas libres. L'auteur souligne également l'importance de prendre du recul et de comprendre les structures mathématiques pour résoudre efficacement ce type d'exercice.
Maths
Algèbre
MPSI/PCSI

Famille recomposée
Résumé SEO-friendly :
Ce cours présente un exercice visant à déterminer si une famille de vecteurs est libre. La famille est construite à partir d'éléments précédents en utilisant des combinaisons linéaires. On pose des réels λ1, λN et on réécrit les équations en fonction de ces coefficients. On cherche à exprimer les coefficients en fonction de λN pour déterminer si la famille est libre. Cependant, l'exercice se complique car il faut tenir compte de la parité des indices. Pour faciliter les calculs, l'enseignant recommande d'utiliser des points de suspension plutôt que des sommes. Finalement, il démontre que si le nombre d'éléments dans la famille est pair, alors la famille est liée, tandis que si le nombre d'éléments est impair, alors la famille est libre. Il souligne l'importance de rester concentré et organisé lors de la résolution d'exercices de ce type.
Maths Approfondies
Algèbre
ECG

Famille libre
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Famille liée
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG
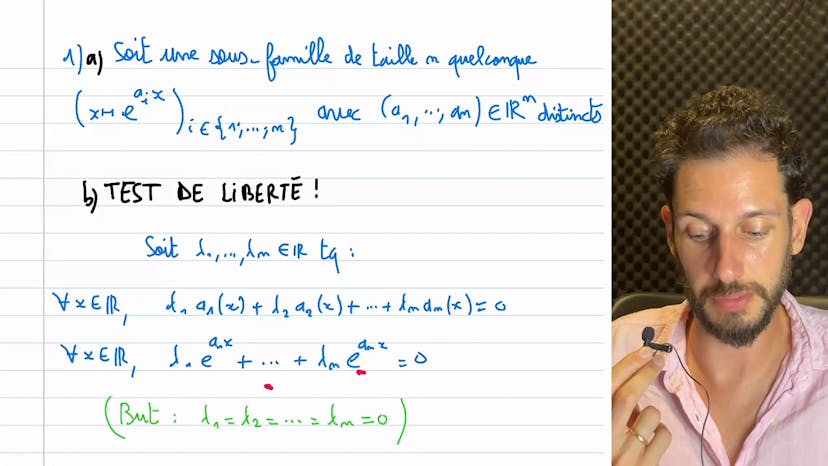
Liberté et familles de fonctions
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG
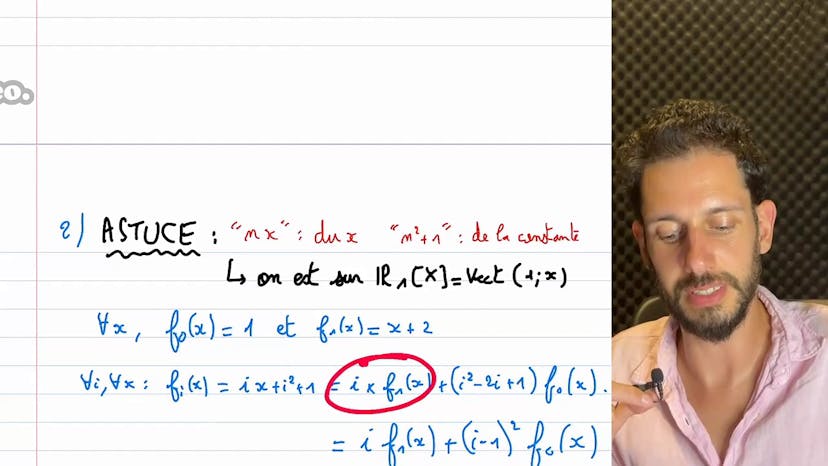
Encore des familles de fonctions
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Famille recomposée
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG

Famille libre
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG

Famille liée
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG
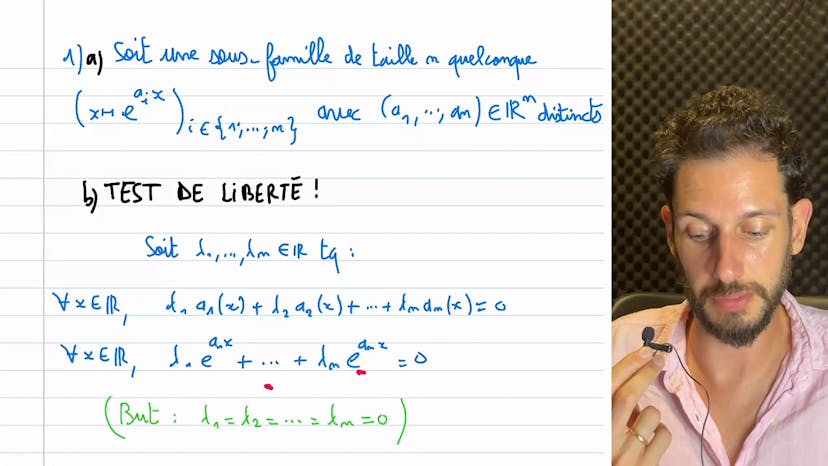
Liberté et familles de fonctions
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG
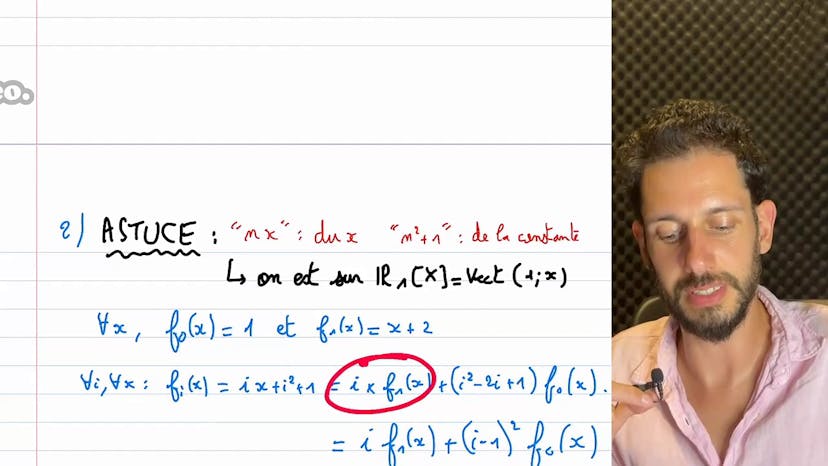
Encore des familles de fonctions
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG

Famille recomposée
Aucun résumé n'est disponible pour cette vidéo


