Cours de Généralités sur les Probabilités en Ligne par les Meilleurs Professeurs - Généralités sur les Probabilités

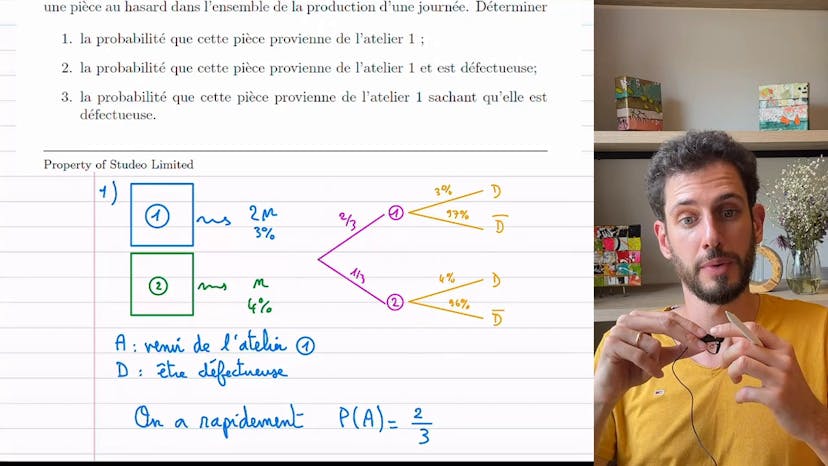
Deux ateliers

L'exercice consiste à analyser deux ateliers d'une entreprise qui fabriquent des pièces. L'atelier 1 produit deux fois plus de pièces que l'atelier 2, mais l'atelier 2 a un pourcentage de pièces défectueuses plus élevé (4% contre 3% pour l'atelier 1). Pour mieux comprendre la situation, il est recommandé de faire un dessin représentant les probabilités. En utilisant cet arbre, on constate que sur 3N pièces, 2N viennent de l'atelier 1, ce qui signifie que la probabilité de prélever une pièce de l'atelier 1 est de 2/3. Ensuite, on aborde les différentes questions. La probabilité que la pièce provienne de l'atelier 1 ET soit défectueuse est calculée en utilisant la formule du cours : P(D inter A) = P(D|A) * P(A). Dans ce cas, la probabilité est de 2%. Pour la troisième question, qui demande la probabilité que la pièce provienne de l'atelier 1 sachant qu'elle est défectueuse, on utilise la formule de Bayes. On calcule d'abord la probabilité d'avoir une pièce défectueuse en utilisant la formule des probabilités totales. On obtient ainsi une probabilité de 10/3, soit environ 3,33%. En utilisant cette information, on peut ensuite calculer la probabilité recherchée (P(A|D)), qui est de 60%. En conclusion, il est important de bien retenir ces formules, de faire un dessin pour représenter la situation et de poser des questions si nécessaire.

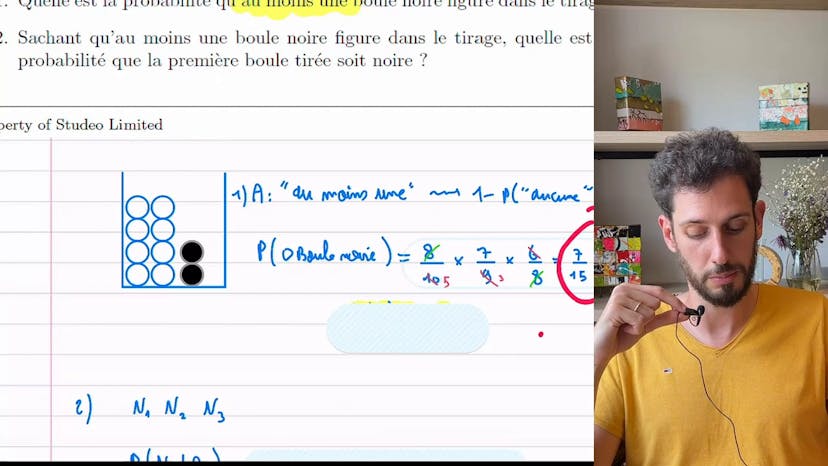
À partir de dénombrement

Ce cours présente un problème de probabilité concernant le tirage de boules d'une urne. Dans cette urne, il y a 8 boules blanches et 2 boules noires. On effectue 100 tirages successifs de 3 boules. L'objectif est de calculer la probabilité d'avoir au moins une boule noire dans le tirage. Pour résoudre ce problème, on commence par calculer la probabilité d'avoir zéro boule noire dans le tirage. Pour cela, on multiplie la probabilité d'avoir une boule blanche lors du premier tirage (8/10) par la probabilité d'avoir une autre boule blanche lors du deuxième tirage (7/9), puis par la probabilité d'avoir une troisième boule blanche lors du troisième tirage (6/8). On obtient ainsi une probabilité de 7/15. La probabilité d'avoir au moins une boule noire est donc égale à 1 - 7/15, ce qui donne 8/15. Ensuite, on s'intéresse à la probabilité que la première boule tirée soit noire, sachant qu'au moins une boule noire figure dans le tirage. On utilise la formule de Bayes pour calculer cette probabilité conditionnelle. On obtient finalement une probabilité de 3/8. Ceci résume le cours de manière SEO friendly, en mettant en évidence les mots clés importants du sujet, à savoir : tirage, boules, probabilité, au moins une, urne.

Formule de Bayes

On a un gérant de magasin d'informatique qui a reçu un lot de clés USB. 5% des boîtes sont abîmées. Le gérant estime que 60% des boîtes abîmées contiennent au moins une clé défectueuse. 98% des boîtes non abîmées ne contiennent aucune clé défectueuse. Un client achète une boîte du lot. On cherche à calculer les probabilités suivantes : P(A), P(~A), P(D|A), P(D|~A), P(~D|A), P(~D|~A), et P(D). En utilisant la formule des probabilités totales, on obtient P(D) = 4,9%. Si un client constate qu'une clé achetée est défectueuse, la probabilité qu'il ait acheté une boîte abîmée est de 61,2%. Il y a donc 40% de chances qu'une clé défectueuse provienne d'une boîte non abîmée.

Questionnaire de Bayes

Dans cette vidéo, on aborde un problème de probabilités lié à un QCM de mathématiques. Le contexte est un peu drôle car il s'agit de déterminer la probabilité qu'un étudiant qui a répondu correctement connaissait réellement la réponse. On pose donc plusieurs événements : C pour "l'étudiant connaît la réponse" et J pour "l'étudiant a eu juste". On utilise ensuite la formule des probabilités conditionnelles pour calculer la probabilité que l'étudiant connaisse la réponse en fonction de la probabilité qu'il ait juste. Si l'étudiant connaît la réponse (événement C), alors la probabilité d'avoir juste est de P (où P est la probabilité qu'un étudiant connaisse la réponse). Si l'étudiant ne connaît pas la réponse, il a une chance sur M (le nombre de réponses possibles) d'avoir juste. Pour calculer la probabilité que l'étudiant connaisse la réponse sachant qu'il a eu juste (événement C sachant J), on utilise la formule des probabilités conditionnelles. On obtient alors P de C sachant J = P / (MP / (1 + MP - P(1/M)). Cet exercice permet de mettre en évidence les liens entre les différentes probabilités et d'utiliser des formules mathématiques pour les calculs.