Cours de Probabilités et échantillonage en Ligne par les Meilleurs Professeurs - Probabilités et échantillonage

Comprendre ∩ et ∪

Dans cet exercice sur les probabilités, on manipule les relations entre événements et leurs contraires. On a deux événements S et T, avec P de S égal à 0,5, P de T égal à 0,6 et P de S union T égal à 0,9. On utilise des formules comme P de A inter B, P de A complémentaire, P de A inter B bar et P de A union B bar pour résoudre les questions de l'exercice. On trouve que P de S inter T est égal à 0,2, P de S union T bar est égal à 0,1 et P de S union T est égal à 0,8.

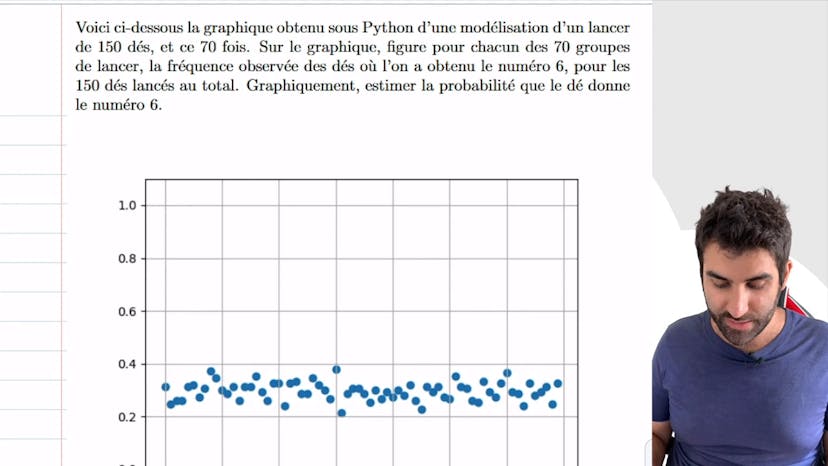
Proba à partir d'une stat ?

Dans cet exercice, on exploite le graphique d'une modélisation de lancé de dés. Nous avons lancé 150 dés 70 fois et chaque groupe de lancés a été représenté graphiquement avec la fréquence du numéro 6. La probabilité d'obtenir un 6 est estimée à environ 30%, ce qui est visible sur le graphique en observant la ligne correspondant à une fréquence de 0,3.

On joue à pile ou face !

Dans cet exercice, on réalise trois expériences aléatoires avec une pièce de monnaie et pour chaque expérience, on doit donner la loi de probabilité, c'est-à-dire la probabilité de chaque issue possible. Pour la première expérience, on fait un seul lancé et on note si c'est face ou pile, chaque option ayant une probabilité de 0,5. Pour la deuxième, on effectue deux lancés et on note l'ordre d'apparition des faces. Il y a quatre issues possibles avec une probabilité de 0,25 chacune. Pour la troisième expérience, on effectue deux lancés et on ne note pas l'ordre d'apparition des faces. Il y a trois options possibles avec une probabilité de 0,25 pour deux piles, 0,5 pour un pile et un face, et 0,25 pour deux faces.

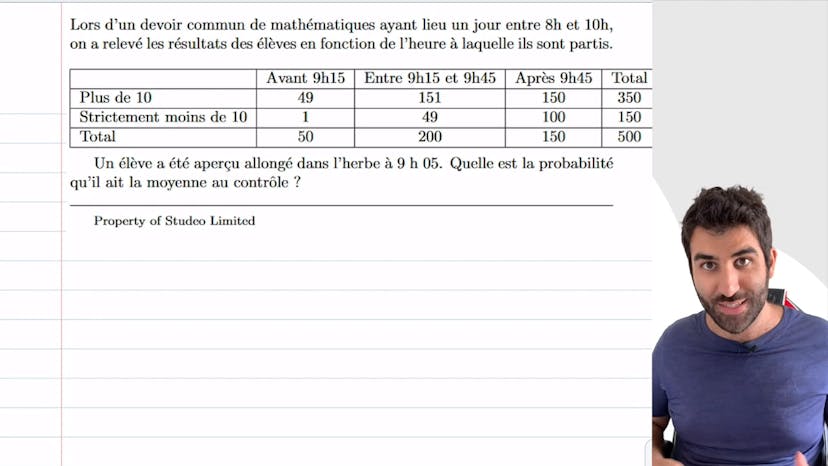
Lire un tableau de données

Dans cet exercice, nous apprenons comment utiliser un tableau de données pour déterminer la probabilité d'un événement. En l'occurrence, le contexte ici est un devoir et les notes obtenues par les élèves selon l'heure à laquelle ils ont quitté le contrôle. La question posée est la suivante : quelle est la probabilité qu'un élève allongé dans l'herbe à 9h05 ait la moyenne ? En analysant la colonne correspondante, nous en déduisons que la probabilité est de 49 sur 50 car l'élève est parti avant 9h15 et a donc plus de 10.

Arbre de probabilités

Dans cet exercice, on cherche à savoir la probabilité d'obtenir exactement une boule blanche à l'issue de deux lancers. Pour y parvenir, on modélise la situation avec un arbre de probabilité en prenant en compte la remise des boules après chaque tirage. En examinant les différents cheminements possibles, seuls deux cas de figure nous intéressent : boule noire puis boule blanche et boule blanche puis boule noire. La probabilité de chacun de ces deux cas de figure est de 6 sur 25 et on obtient une probabilité de 12 sur 25 en additionnant les deux. Ainsi, la probabilité de tirer exactement une boule blanche est de 12 sur 25.