 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Nombres et Calcul numérique
- Intervalles et Inégalités
- Identités remarquables et équations
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Nombres et Calcul numérique
- Intervalles et Inégalités
- Identités remarquables et équations
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Nombres et calculs
Seconde

Système d'inégalités
Dans cet exo, on apprend à résoudre deux inéquations et à trouver une solution qui vérifie une inéquation mais pas l'autre. Pour résoudre les inéquations, on applique des opérations mathématiques et on obtient des intervalles I et J. Ensuite, on trace une droite graduée et on place les valeurs charnières des intervalles, à savoir -3/2 et 11/2. On voit que ce qui est en commun entre les intervalles I et J, c'est l'intervalle [-3/2, 11/2]. Ainsi, pour trouver une solution qui vérifie une inéquation mais pas l'autre, on prend un nombre qui est dans cet intervalle, mais qui n'est pas dans l'autre intervalle. Par exemple, A = 10 convient.
Maths
Nombres et calculs
Seconde

Comparer des expressions de x
Dans cet exo, on apprend comment comparer deux expressions numeriques A et B. La méthode consiste à trouver la différence entre A et B, puis à étudier le signe du résultat. Si A moins B est négatif, alors A est plus petit que B. Si A moins B est positif, alors A est plus grand que B. Et si A moins B est égal à 0, alors A et B sont égaux. Pour trouver le signe de A moins B, on examine l'expression MX plus P, où M est le coefficient de X et P est la constante. Si M est positif, alors l'expression affine est positive sur un intervalle. Si M est négatif, alors l'expression affine est négative sur l'intervalle. En utilisant cette méthode, on peut conclure que A est plus petit que B sur un certain intervalle, A est égal à B à un certain point et A est plus grand que B sur un autre intervalle.
Maths
Nombres et calculs
Seconde

Résoudre une inéquation
Dans cet exercice, on apprend à résoudre une inéquation basique en isolant x. On doit notamment faire attention à changer le sens de l'inégalité quand on multiplie ou divise par un nombre négatif, et à appliquer les règles de la transformation d'un terme d'un côté à l'autre de l'inéquation. Ainsi, pour résoudre l'inéquation donnée, on procède à des calculs pour se débarrasser des termes en trop, en changeant le signe ou en divisant selon les cas. Finalement, on obtient la solution sous forme d'un intervalle. Dans ce cas, la solution est x supérieur ou égal à 1, ce qui correspond à l'intervalle fermé allant de 1 à l'infini.
Maths
Nombres et calculs
Seconde
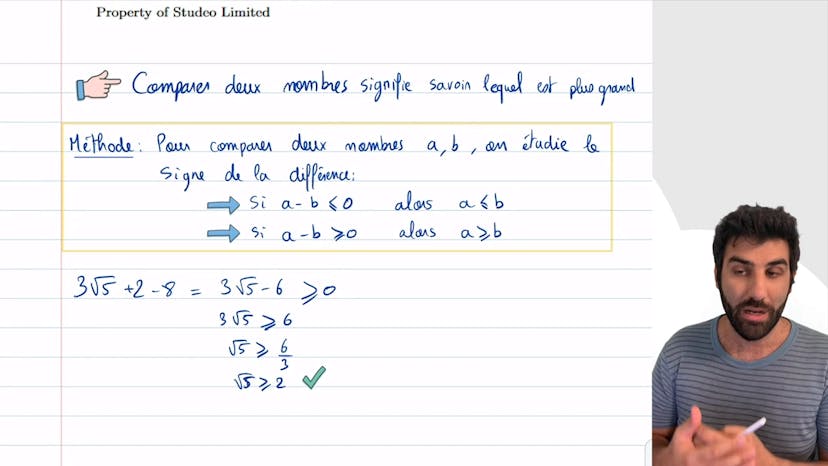
Comparer des racines
Dans cet exo, nous allons comparer trois nombres sans utiliser une calculatrice. La méthode pour cette comparaison est de soustraire le plus petit nombre du plus grand et vérifier si le résultat est positif ou négatif. Nous allons tester la méthode avec les nombres 3 racines de 5, 2 et 8. En simplifiant 3 racines de 5 moins 6, nous obtenons 3 racines de 5 supérieur égal à 6 sur 3, qui est égal à racine de 5 supérieur égal à 2. Nous pouvons donc conclure que 3 racines de 5 plus 2 est plus grand que 8. Si le résultat avait été différent, nous aurions recommencé en utilisant des inégalités opposées.
Maths
Nombres et calculs
Seconde
Inégalité triangulaire bien dure !
Aucun résumé n'est disponible pour cette vidéo


