 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Nombres et Calcul numérique
- Intervalles et Inégalités
- Identités remarquables et équations
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Nombres et Calcul numérique
- Intervalles et Inégalités
- Identités remarquables et équations
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Nombres et calculs
Seconde

Différentes écritures de f
Dans cet exercice, on part d'une fonction f(x) = (x+2)² - 9, et on cherche à la décomposer en forme développée et en forme factorisée. On utilise ensuite ces formes pour calculer f(3), f(√3 - 2), résoudre f(x) = 0 et trouver les antécédents de -5 par f. Pour cela, on utilise principalement la forme canonique et la forme factorisée, et on factorise en identité remarquable. Les antécédents de -5 par f sont 0 et -4.
Maths
Nombres et calculs
Seconde

Détecter une identité remarquable
Dans cette transcription d'une vidéo, on apprend comment résoudre une équation du second degré en factorisant avec un facteur commun ou une identité remarquable. On montre comment identifier les termes a², 2ab et b² pour utiliser l'identité remarquable numéro 2. On vérifie que la factorisation obtenue est correcte et on résout l'équation obtenue en isolant x. La solution trouvée est x égale à 5 demi.
Maths
Nombres et calculs
Seconde

Equation produit nul
Dans cet exercice, nous voyons comment résoudre une équation produit nul, c'est-à-dire lorsque le produit de facteur est égal à 0 et qu'au moins un des facteurs est nul. La méthode consiste à regarder chaque facteur et à voir quand il s'annule. Nous appliquons cette méthode à une équation donnée, x²-9 facteur de x plus 20 égal à 0. Nous trouvons que les solutions sont x égale à moins 20, 3 ou moins 3. Nous utilisons également la méthode pour trouver les solutions de x² égale k, ce qui nous permet de trouver les solutions de l'équation de départ. Ainsi, x² moins 9 facteur de x plus 20 est égal à 0 a pour solution moins 20, moins 3 et 3.
Maths
Nombres et calculs
Seconde

Factoriser pour résoudre
Dans cet exercice, on utilise la méthode du changement de variable pour résoudre une équation. En remplaçant X par x², l'équation x4 + x² = 6 devient X² + X - 6 = 0. Ensuite, on utilise la formule du produit de facteurs nuls pour trouver les solutions possibles : X = 2 ou X = -3. En ramenant X à x, on obtient finalement les deux solutions réelles X = racine de 2 ou X = -racine de 2.
Maths
Nombres et calculs
Seconde

Factoriser avec a²-b²
Dans cet exercice, on apprend à factoriser à l'aide des trois identités remarquables : a plus b au carré, a moins b au carré, et a moins b facteur de a plus b. Pour factoriser une expression, on doit identifier les termes et choisir l'identité remarquable correspondante. Ensuite, on peut utiliser les formules pour trouver la valeur de a et la valeur de b, puis écrire l'expression sous forme de a-b fois a plus b. Dans l'exemple donné, on factorise l'expression 4x²-16 en utilisant l'identité remarquable numéro 3. On obtient finalement 2x-4 fois 2x plus 4.
Maths
Nombres et calculs
Seconde

Factorisation multiple
Dans cet exercice de mathématiques, on cherche à factoriser une expression compliquée en utilisant des identités remarquables. Après avoir examiné les termes et les signes, on identifie que l'expression x² + 6x + 9 peut être factorisée en (x + 3)². Ensuite, on utilise cette identité remarquable pour factoriser l'expression de départ en (x + 3) (x + 3 - 2x + 3). En regroupant les termes, on obtient finalement l'expression factorisée en x + 3 ( -x + 6).
Maths
Nombres et calculs
Seconde

Produit en croix
Dans cet exercice, on apprend à résoudre une équation avec une égalité de fractions en la transformant en produit. Après avoir développé l'équation, le second degré s'en va, permettant de résoudre l'équation classiquement. Avec X différent de -1,5 et 1, la solution est trouvée grâce à une opération de division. L'équation de départ avec les fractions a pour solution X égal à 3 sur 5.
Maths
Nombres et calculs
Seconde
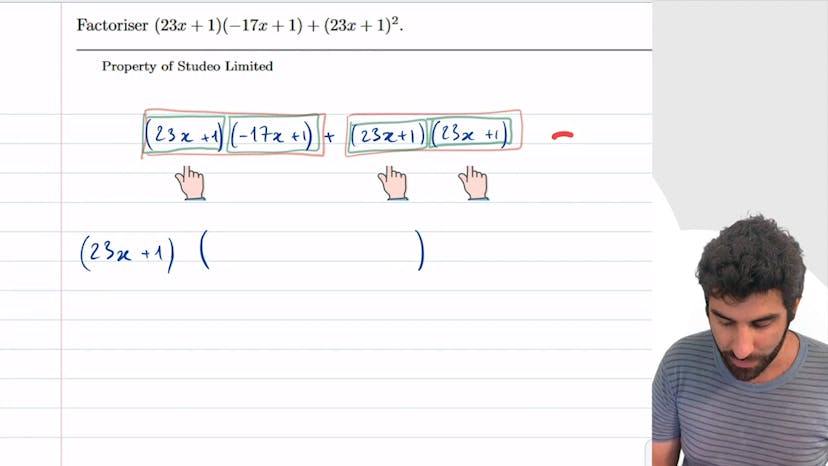
Reconnaître un facteur commun
Dans cet exercice de maths, la méthode pour factoriser une expression utilisée consiste à réécrire l'expression pour trouver tous les facteurs qu'elle contient. Ensuite, on repère les termes en commun dans les deux côtés de l'expression. On met ces termes communs en parenthèses et on distribue le reste des termes en soustrayant les facteurs communs. Enfin, on simplifie et on regroupe pour obtenir la forme factorisée. En appliquant cette méthode, l'expression 23x² + 46x + 21 peut être factorisée en (23x + 1)(6x + 2).


