 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Analyse
2BAC SM Maroc

Encore un taux d'accroissement de exp
Dans ce cours, nous étudions le calcul des limites, en prenant l'exemple de lim(x→+∞) e^(1/x) - x.
Tout d'abord, lorsque x tend vers +∞, le terme e^(1/x) tend vers 0, ce qui signifie que le tout tend vers 1.
Ensuite, on cherche à factoriser par x. En effectuant cette opération, on obtient e^(1/x) - 1.
Cependant, malgré cette simplification, on se retrouve toujours avec une forme indéterminée. Il faut donc aller plus loin.
En utilisant une astuce, on pose x = 1/(1/x). Ainsi, on peut réécrire l'expression comme e^(1/x) - 1.
En simplifiant cette nouvelle expression, on obtient e^(1/x) - 1/(1/x). Et comme 1/x tend vers 0, la limite est égale à 1.
Donc, la limite de la fonction e^(1/x) - x, lorsque x tend vers +∞, est égale à 1.
Ce type d'exercice peut sembler complexe, car il nécessite de repérer des formules et de les utiliser de manière astucieuse pour trouver la solution. Il est donc important d'avoir une connaissance approfondie des formules et de savoir les appliquer dans des contextes variés.
Maths SM&SP
Analyse
2BAC SM Maroc

Introduction Convergence
Dans ce cours sur les limites de fonctions, nous allons aborder des concepts pratiques tels que les tableaux de fonctions de référence et les combinaisons de limites. Il sera important de connaître par cœur certains tableaux, par exemple la limite de 1 sur x en plus infini. Nous étudierons également des cas plus complexes, où une fonction tend vers l'infini et une autre vers moins l'infini. Dans ce contexte, nous analyserons le rapport entre ces fonctions et leur produit.
Parmi les règles à connaître, il y en aura quatre appelées "formes indéterminées" pour lesquelles il n'existera pas de règles préétablies. Ces cas particuliers constitueront une source d'exercices et de pièges, il sera donc important de les comprendre et de les maîtriser.
Nous aborderons également des théorèmes de convergence, similaires à ceux appliqués aux suites. Par exemple, le théorème des gendarmes, où deux fonctions encadrent une troisième et l'amènent vers la même limite finie. Il y aura également le théorème de comparaison pour les limites infinies, qui explique que si une fonction est "plus petite" qu'une autre et tend vers l'infini, alors cette dernière la suivra dans sa limite.
Nous étudierons également la croissance comparée, en comparant la limite de l'exponentielle avec des polynômes, ainsi que les limites de fonctions composées. Pour les fonctions plus complexes, nous utiliserons des méthodes de décomposition en sous-blocs pour analyser leur limite.
En résumé, il sera important de reconnaître les tableaux de référence pour les fonctions, de comprendre les opérations sur les limites et de mémoriser les quatre formes indéterminées. Les théorèmes de comparaison, des gendarmes, de croissance comparée et les limites des fonctions composées seront également à maîtriser.
En termes de méthodes, nous présenterons deux approches pratiques pour gérer les formes indéterminées, notamment l'utilisation du terme du plus haut degré et la méthode de quantité conjuguée.
En conclusion, une fois que vous aurez assimilé ces points de cours et ces méthodes, vous serez prêts à aborder les différents types de limites que nous vous présenterons. N'hésitez pas à poser des questions dans la FAQ ou à consulter les discussions déjà existantes sur les sujets qui vous intéressent. À bientôt !
Maths SM&SP
Analyse
2BAC SM Maroc

Tableaux : fonctions de référence
Dans cette vidéo, nous faisons un bilan des différentes fonctions de référence en mathématiques et de leurs limites. Nous examinons également les règles pour les combinaisons de limites, telles que la somme, le produit et le quotient. Nous commençons par étudier la fonction 1/x et expliquons que sa limite devient plus ou moins l'infini lorsque x approche à la fois positif et négatif. Ensuite, nous examinons les limites de la fonction x^n, où n est un nombre entier, et montrons graphiquement comment ces fonctions tendent vers l'infini lorsque x devient de plus en plus grand. Nous discutons également de l'exponentielle et de la racine carrée, montrant comment ces fonctions évoluent graphiquement. Enfin, nous expliquons comment manipuler ces fonctions en prenant en compte le signe de l'exposant ou de l'exponentielle et comment cela peut affecter les limites. Nous encourageons les spectateurs à retenir ces propriétés et à consulter la FAQ pour plus d'informations.
Maths SM&SP
Analyse
2BAC SM Maroc

Tableaux : combiner des limites
Le cours traite principalement des limites d'une somme et d'un produit, en utilisant des exemples simples pour illustrer les concepts. Globalement, on constate que lorsque les fonctions f et g tendent chacune vers une limite L et L', la somme tend vers L + L' et le produit tend vers L * L'. De plus, lorsque l'une des limites est infinie, elle l'emporte toujours. Par exemple, si L est positif, le produit tendra vers l'infini et s'inversera si L est négatif. Il est important de retenir que ces exemples ont du sens, mais il existe deux cas indéterminés où il est difficile de déterminer ce qui se passe : la multiplication de 0 par l'infini et l'addition de l'infini positif et de l'infini négatif. Une forme indéterminée signifie qu'il n'y a pas de règle fixe et que différents résultats sont possibles. Le quotient de fonctions suit des règles similaires, avec des résultats différents en fonction des limites. Les formes indéterminées à retenir sont 0 sur 0 et l'infini sur l'infini. Il est recommandé de s'entraîner à créer des exemples simples pour faciliter la compréhension. La vidéo couvre l'essentiel du sujet et insiste particulièrement sur les formes indéterminées, qui nécessitent une attention particulière.
Maths SM&SP
Analyse
2BAC SM Maroc
Comparaison et encadrement
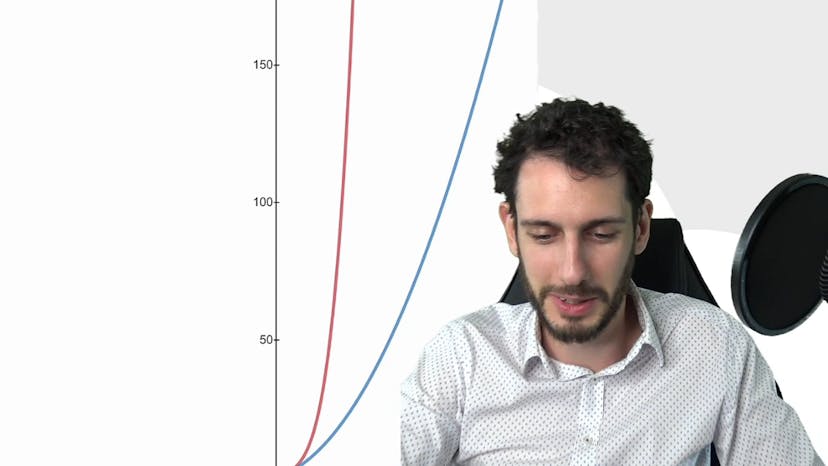
Ce cours présente deux théorèmes de comparaison en mathématiques, qui permettent de comparer des fonctions et de déterminer leurs comportements asymptotiques. Le premier théorème de comparaison stipule que si deux fonctions f et g sont telles que f tend vers l'infini et g est plus grande que f, alors f va "pousser" g et les deux fonctions tendront vers l'infini. Un exemple est donné pour illustrer ce théorème en prenant les fonctions f(x) = x²/4 + x et g(x) = x²/4 + x²/32. Il est montré graphiquement que g(x) est toujours au-dessus de f(x) et que si f tend vers l'infini, alors g tendra également vers l'infini.
Le deuxième théorème présenté est le théorème des gendarmes, également appelé théorème d'encadrement. Ce théorème est basé sur le concept d'encadrement d'une fonction entre deux autres fonctions. Si f et h encadrent une fonction g telle que f est inférieure à g et g est inférieure à h, et que les limites de f et h sont égales à un réel L, alors la limite de g sera également égale à L. Une illustration graphique est donnée pour montrer comment les deux fonctions encadrent une troisième fonction et que si les limites de f et h sont les mêmes, la limite de g sera également la même.
En conclusion, ces théorèmes de comparaison sont utiles pour comparer et étudier le comportement des fonctions en s'inspirant de fonctions "plus jolies" et pour déterminer leurs limites. Ils sont particulièrement utiles dans les exercices mathématiques.
Maths SM&SP
Analyse
2BAC SM Maroc
Croissance comparée exp et ln
Dans ce cours, nous étudions la croissance comparée et les limites de fonctions. La croissance comparée est l'idée selon laquelle l'exponentiel dominera toujours sur les puissances de x, peu importe leur valeur. Par exemple, si nous prenons l'exponentiel de x divisé par x puissance 7000, nous pourrions penser que cette expression tendra vers 0, mais en réalité, l'exponentiel domine complètement sur les puissances de x et tendra vers l'infini.
Nous pouvons également observer cette domination en examinant le graphique de l'exponentiel. Il monte rapidement vers l'infini et s'écrase rapidement vers zéro. Par conséquent, même les puissances de x comme x2 ou x3 seront éventuellement dépassées par l'exponentiel.
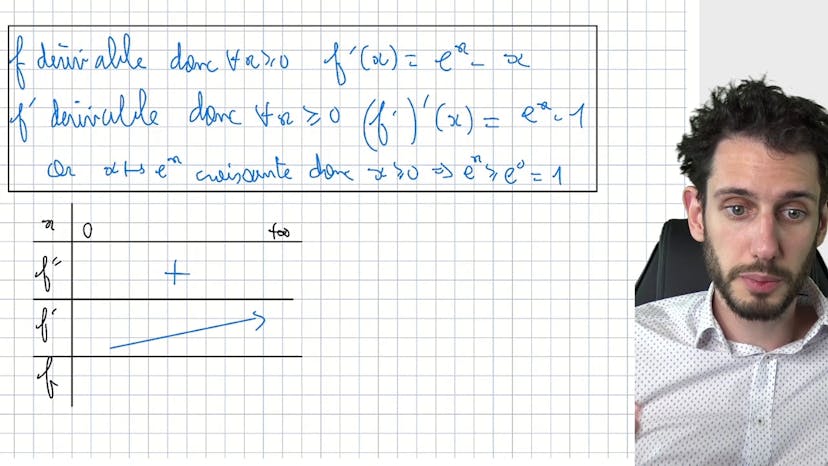
Pour démontrer la croissance comparée de manière générale, nous utilisons le théorème de comparaison. Nous prouvons d'abord le cas particulier de E2x/x tendant vers l'infini à l'aide du tableau de variation de la fonction. Ensuite, nous utilisons ce résultat pour démontrer le cas général avec n étant un entier quelconque. Nous utilisons des astuces de changement de variable et les propriétés des puissances pour simplifier les expressions et prouver finalement que E(x/n)^n tend vers l'infini
Maths SM&SP
Analyse
2BAC SM Maroc

Limite des fonctions composées
Le chapitre des limites de fonctions aborde le concept de composition de fonctions. On commence par un exemple concret : trouver la limite de racine de (1 + e^x) lorsque x tend vers l'infini. Pour cela, on décompose la fonction en deux parties : d'abord la fonction f(x) = 1 + e^x, puis ensuite on ajoute la racine. On souhaite démontrer que cette limite est égale à 1.
Cependant, il faut rappeler qu'il faut utiliser un théorème mathématique pour justifier cette démarche. On ne peut pas simplement rajouter la racine de manière intuitive, il faut le prouver. Le théorème en question permet de composer deux fonctions et d'obtenir leur limite. La rédaction de cette démonstration consiste à considérer d'abord la limite de la première fonction f(x) = 1 + e^x, qui tend vers 1 lorsque x tend vers moins l'infini. Ensuite, on s'intéresse à la limite de la fonction racine en 1. On conclut alors que la limite de racine de f(x) est égale à 1.
La formule générale du théorème énonce que si la limite de f(x) est b lorsque x tend vers a, et si la limite de g(x) est c lorsque x tend vers b, alors la limite de la composition g(f(x)) lorsque x tend vers a est égale à c.
En résumé, ce chapitre aborde la notion de composition de fonctions pour trouver des limites. Il est important de se rappeler qu'il faut utiliser un théorème pour justifier cette démarche.
Maths SM&SP
Analyse
2BAC SM Maroc

Forme indéterminée : utilisation du terme plus haut degré
Dans ce cours, nous allons voir comment déterminer les limites infinies des polynômes et des fonctions rationnelles.
La méthode à utiliser est la factorisation par le terme de plus haut degré, appelé "terme de Claudegris". Ce terme sera le seul à prendre en compte pour déterminer la limite.
Prenons l'exemple de la fonction G(x) = x^4 + 4x^2 - 2x. On peut voir que cette fonction a une forme indéterminée, car pour x tendant vers plus ou moins l'infini, la somme des termes tend vers l'indéterminé.
En factorisant par x^4, on obtient : G(x) = (1 + 4/x^2 - 2/x^3). Peu importe que x tende vers plus ou moins l'infini, cette expression tend vers 0. Ainsi, x^4 tend vers plus l'infini.
Pour une fonction rationnelle ayant un quotient de deux polynômes, la méthode est la même. On factorise le numérateur et le dénominateur par le terme de plus haut degré.
Prenons l'exemple de la fonction rationnelle H(x) = 2x^2 / (1 - x). En factorisant le dénominateur par le terme de Claudegris, x, on obtient : H(x) = 2x / (x - 1/x).
Cette expression tend vers -1, que ce soit pour x tendant vers plus ou moins l'infini. Ainsi, le quotient de 2x par (x - 1/x) tend vers moins l'infini pour x tendant vers moins l'infini, et vers plus l'infini pour x tendant vers plus l'infini.
En résumé, il suffit de factoriser par le terme de plus haut degré pour résoudre les indéterminations des polynômes et des fonctions rationnelles. Il est important de maîtriser cette méthode qui fonctionne à tous les coups. N'hésitez pas à vous entraîner si vous avez encore des doutes.
Maths SM&SP
Analyse
2BAC SM Maroc

Forme indéterminée : Méthode quantité conjuguée
La méthode de la quantité conjuguée est utilisée lorsque nous avons des racines dans une équation. Les racines ne s'additionnent pas bien, donc nous essayons souvent de multiplier la quantité conjuguée pour les supprimer. Dans l'exemple donné, nous avons une fonction avec une forme indéterminée lorsque x approche de 0. Cependant, lorsque x est proche de 0+, le terme devient 1/1, ce qui n'est pas indéterminé. Cependant, lorsque nous approchons de l'infini, la forme devient indéterminée. Dans ce cas, nous utilisons la quantité conjuguée en multipliant le numérateur et le dénominateur par la quantité conjuguée. Cela fait disparaître les racines du dénominateur, mais en fait apparaître dans le numérateur. Cependant, le fait d'obtenir un plus au lieu d'un moins dans le numérateur rend la forme non indéterminée. Dans l'exemple donné, nous obtenons une expression simplifiée sans dénominateur, qui est racine de x plus 1 plus racine de x. Cette forme n'est plus indéterminée et tend vers l'infini lorsque nous approchons de l'infini. La méthode de la quantité conjuguée est une méthode classique utilisée lorsque nous analysons des équations avec des racines.
Maths SM&SP
Analyse
2BAC SM Maroc

Limites : la Croissance comparée
La croissance comparée est une méthode très utile en mathématiques. Lorsque nous étudions la fonction e de x sur x, nous pouvons observer que lorsque x tend vers moins l'infini, cette fonction tend vers 0. De plus, grâce à la croissance comparée, nous savons que e de x l'emporte sur toute puissance de x, ce qui signifie que même lorsque x tend vers plus l'infini, cette fonction tendra toujours vers plus l'infini.
Ensuite, nous étudions une autre fonction appelée h. En utilisant la croissance comparée, nous pouvons transformer cette fonction en une formulation plus simple, en posant grand x égal à x. Ainsi, lorsque x tend vers moins l'infini, grand x tend vers plus l'infini, ce qui nous permet de simplifier la fonction. Par composition des limites, nous pouvons déduire que cette fonction tendra vers 0 lorsque x tend vers moins l'infini.
En général, la croissance comparée nous permet de déterminer rapidement le comportement de différentes fonctions. L'exponentielle l'emporte sur toutes les puissances de x, tandis que le logarithme perd toujours contre les puissances de x. Il est important de se rappeler de ces références de croissance comparée pour résoudre plus facilement les problèmes.
Si vous avez des questions supplémentaires, n'hésitez pas à consulter la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

Double racine
Bonjour à tous, je vais corriger cet exercice sur les limites. C'est un exercice de difficulté intermédiaire qui porte sur l'étude des limites d'une fonction f(x) = √(x) + √(1+x²).
Tout d'abord, il est important de déterminer sur quel ensemble de définition la fonction est définie. Pour cela, nous devons vérifier que les racines sont bien définies.
Dans un premier temps, nous vérifions que la racine la plus imbriquée (√(1+x²)) est définie pour tout x réel. En observant l'expression, nous constatons que pour tout x réel, 1+x² est toujours positif, donc il n'y a pas de problème pour la première racine.
Ensuite, nous regardons la deuxième racine (√(x+√(1+x²))). Si x est supérieur à 0, il n'y a aucun problème car x est positif et la racine est également positive. Si x est inférieur à 0, nous devons comparer les deux termes. En utilisant l'inégalité 1+x² > x², nous pouvons prendre la racine des deux côtés. Ainsi, nous obtenons √(1+x²) > |x|, ce qui signifie que x est négatif. Donc, l'intérieur de la racine est positif et la racine est définie pour tout x réel.
Nous concluons que la fonction f est définie sur l'ensemble des réels.
Ensuite, nous étudions le tableau de variation de la fonction. Pour cela, nous devons justifier la dérivabilité de la fonction sur tout l'ensemble des réels.
La fonction racine n'est pas dérivable en 0 car elle a une pente infinie à cet endroit. Donc, nous devons étudier cela de plus près. En simplifiant l'expression de la fonction, nous constatons que l'intérieur des racines doit être strictement positif. Nous avons déjà montré cela précédemment. Donc, la fonction f est dérivable sur tout l'ensemble des réels.
Calculons maintenant la dérivée de la fonction. En posant u(x) = x + √(1+x²), nous dérivons cette fonction et obtenons u'(x) = (√(1+x²) + x) / √(1+x²). En utilisant les formules de dérivation pour les racines, nous obtenons la dérivée de f qui est égale à (√(1+x²) + x) / 2√(1+x²).
Nous constatons que le terme au numérateur et le terme au dénominateur sont strictement positifs. Par conséquent, la dérivée de f est toujours positive et la fonction f est strictement croissante sur tout l'ensemble des réels.
Passons maintenant aux limites de la fonction. La limite de f lorsque x tend vers l'infini est égale à l'infini. En justifiant par composition, nous pou
Maths SM&SP
Analyse
2BAC SM Maroc
Calculs de limites complexes
Bonjour à tous, dans ce cours nous allons aborder des exercices complexes sur les limites. Ces exemples sont destinés à ceux qui souhaitent se préparer pour l'année prochaine.
Le premier exercice concerne des racines, il faut utiliser la quantité conjuguée pour simplifier l'expression. En utilisant cette méthode, on obtient une limite de 1/2.
Le deuxième exercice porte sur des puissances et on remarque que l'expression est indéterminée. En utilisant les taux d'accroissement et la dérivée, on parvient à trouver la limite qui est égale à (n+1)/n.
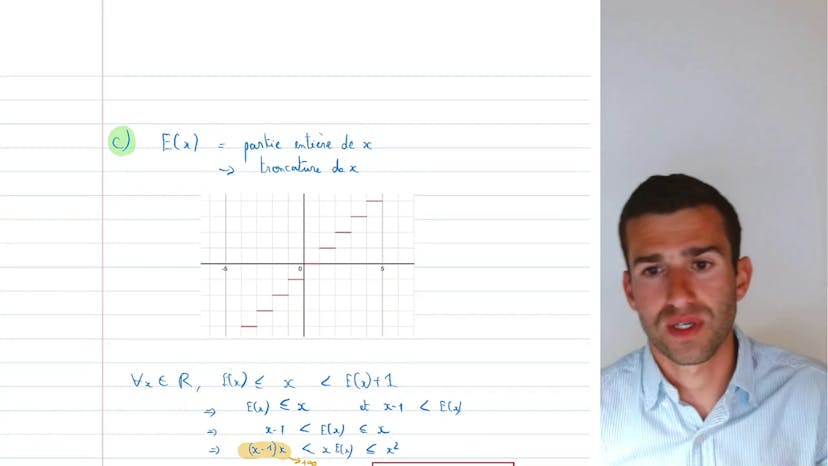
Le troisième exercice fait intervenir la partie entière d'un nombre. En encadrant la fonction, on peut déterminer sa limite qui est l'infini.
Le quatrième exercice est composé de nombreuses racines, il faut utiliser la quantité conjuguée pour simplifier l'expression. En décomposant les termes et en utilisant les taux d'accroissement, on obtient une limite de -1/(2√a).
Ces exercices représentent des exemples complexes qui permettent de se familiariser avec les limites et d'apprendre à les résoudre de manière efficace.


