Cours d'apprentissage en ligne

Inductance mutuelle

Aucun résumé n'est disponible pour cette vidéo

Dans cette vidéo, nous abordons le sujet des machines thermiques, en particulier les machines dithermes. L'objectif de la première vidéo de ce chapitre est d'appliquer les principes de la thermodynamique aux machines dithermes. Le principe général pour résoudre n'importe quelle question portant sur une machine ditherme est le suivant : dans une machine ditherme, tout état thermodynamique (U, H ou S) reste constant sur un cycle. Cela signifie que la variation de ces grandeurs sur un cycle est nulle. À partir de là, nous pouvons déterminer les grandeurs qui nous intéressent, telles que le travail, les transferts thermiques et éventuellement l'efficacité. En appliquant le premier principe de la thermodynamique à un cycle, nous pouvons écrire que la variation de l'énergie interne (delta U) est égale au travail (W) plus les transferts thermiques (Q). Comme nous sommes sur un cycle, la variation de l'énergie interne est nulle. Cela nous donne donc l'équation delta U = W + Q = 0. Le deuxième principe de la thermodynamique est également important dans le cas des cycles. Il nous dit que l'entropie créée est positive lors d'une transformation thermodynamique, et que l'entropie échangée est donnée par Q/T. Comme nous sommes sur un cycle thermodynamique, la variation d'entropie (delta S) est nulle. Donc, nous pouvons écrire delta S comme la différence entre l'entropie échangée (S E) et l'entropie créée (S C), ce qui donne S E = -S C. Comme l'entropie créée est positive, cela signifie que l'entropie échangée est négative, conformément à l'inégalité de Clausius. Si l'égalité est vérifiée, cela signifie que le fonctionnement est réversible. En résumé, ce cours traite des machines thermiques, en mettant l'accent sur les machines dithermes. Les principes de la thermodynamique sont utilisés pour résoudre les questions portant sur ces machines. Le premier principe établit que la variation de l'énergie interne sur un cycle est nulle, tandis que le deuxième principe permet de déterminer l'entropie échangée et créée. L'inégalité de Clausius est une conséquence du second principe.

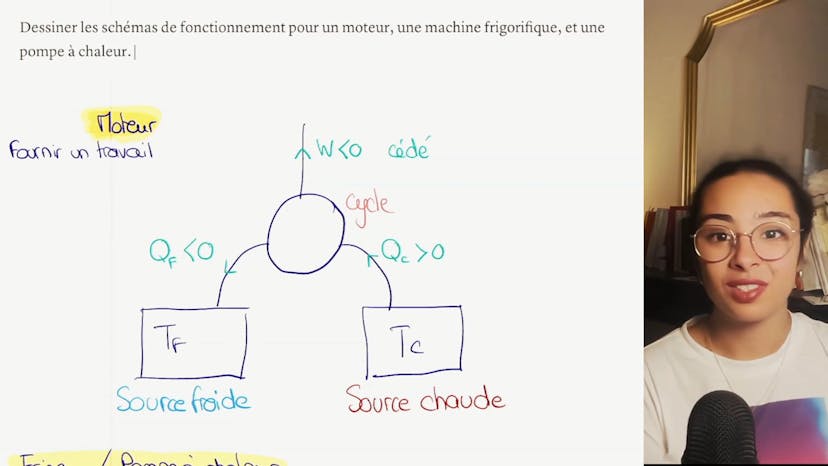
Schéma des machines thermiques

Aujourd'hui, nous allons parler des schémas des machines thermiques, à savoir le moteur, la machine frigorifique et la pompe à chaleur. Le moteur a pour objectif de fournir un travail en utilisant une source froide et une source chaude. Par exemple, dans un moteur diesel, une explosion se produit et génère un travail thermique qui permet à la voiture de se déplacer. Dans le schéma d'une machine thermique, nous avons un cycle avec une source chaude à la température Tc, une source froide à la température Tf, et un travail noté comme Gw. Dans le cas du moteur, le travail est cédé, c'est-à-dire que le cycle fournit un travail et reçoit de l'énergie de la source chaude, puis redonne de l'énergie à la source froide. Pour ce qui est du frigo et de la pompe à chaleur, ils fonctionnent de la même manière. La seule différence réside dans l'emplacement de la source froide. En gros, un climatiseur ou une pompe à chaleur refroidit la source froide encore plus et réchauffe la source chaude encore plus. Dans le schéma d'une pompe à chaleur ou d'un climatiseur, on reçoit du travail électrique, on réchauffe la source chaude (QC est négatif) et on refroidit la source froide (QF est positif). Si l'on souhaite chauffer une maison, on mettra la source chaude dans la maison, tandis que si l'on souhaite refroidir la maison, on mettra la source froide à l'extérieur. En résumé, les machines frigorifiques et les pompes à chaleur refroidissent la source froide et réchauffent la source chaude. Dans les prochaines vidéos, nous aborderons le calcul de l'efficacité et du rendement de ces machines.

Efficacités et rendements

Dans ce cours, on apprend à calculer les efficacités et les rendements des machines thermiques. L'efficacité ou le rendement est défini comme l'énergie utile divisée par l'énergie consommée. Pour un moteur, le rendement est égal à l'énergie utile (W) divisée par l'énergie consommée (QC), et il est toujours inférieur à 1. On utilise les principes du second principe et du cycle de fonctionnement pour éliminer le travail (W) et obtenir l'efficacité en fonction de QF (énergie cédée) et QC (énergie consommée). On peut aussi faire le lien avec les températures en utilisant l'inégalité de Clausius. L'efficacité est donc inférieure à 1-TF/TC, où TF et TC sont les températures respectives de la source froide et de la source chaude. Cette valeur est appelée le rendement de Carnot, qui représente le meilleur rendement possible. Dans le cas d'une pompe à chaleur, on utilise le même procédé pour calculer l'efficacité, qui est égale à moins QC sur W. En utilisant les principes et l'inégalité de Clajus, on trouve que l'efficacité est inférieure à 1- TF/TC. Ces calculs sont importants pour comprendre le fonctionnement des machines thermiques et peuvent être appliqués à des machines plus complexes.

Chauffage d'une maison

Dans cette vidéo, nous faisons un exercice sur le chauffage d'une maison à l'aide d'une pompe à chaleur. L'objectif est de maintenir la température intérieure à 20 degrés alors que la température extérieure est de 5 degrés. L'isolation thermique de la maison nécessite un transfert thermique de 200 kJ par heure. Il est rappelé que la pompe à chaleur reçoit un transfert thermique de la source froide et en fournit un à la source chaude. Pour cela, un travail électrique est nécessaire pour faire fonctionner la pompe à chaleur. L'efficacité maximale de la pompe est atteinte avec le cycle de Carnot, qui fonctionne de manière réversible. L'efficacité de Carnot dépend de la différence de température entre la source froide et la source chaude, et en donner une définition précise. Ensuite, nous calculons la puissance électrique minimale requise par la pompe à chaleur pour assurer un transfert thermique de 200 kJ par heure. Utilisant l'efficacité, nous trouvons que la puissance électrique nécessaire est de 2,8 kW. Nous abordons ensuite la question de la température extérieure pour laquelle l'efficacité de la pompe à chaleur est maximale. L'efficacité est maximale lorsque la différence de température entre la source froide et la source chaude est minimale. Cela signifie que la pompe à chaleur fonctionne plus efficacement lorsque la température extérieure n'est pas trop basse et que la différence de température entre l'intérieur et l'extérieur est faible. En conclusion, il est important de comprendre le fonctionnement d'une pompe à chaleur pour optimiser son efficacité et son utilisation dans le chauffage d'une maison.

Moteur Diesel

Dans cet exercice sur le moteur diesel à double combustion, on nous présente un diagramme de Watt qui représente différentes phases du cycle moteur. Les transformations sont décrites avec des termes spécifiques tels que compression adiabatique, combustion isoc

Réfrégirateur

Aujourd'hui, nous allons résoudre un exercice sur les machines thermiques, plus précisément sur un réfrigérateur. L'exercice consiste à déterminer le travail minimal nécessaire pour transformer 1 kg d'eau liquide à 0°C en glace en utilisant un réfrigérateur. La température de la pièce dans laquelle se trouve le réfrigérateur est de 19°C et est constante. Avant de commencer, il est important de comprendre ce que signifie "travail minimal". En thermodynamique, le fonctionnement optimal d'une machine est souvent celui qui est réversible, comme le rendement de Carnot. Ainsi, pour fournir le moins d'énergie possible, il faut connaître le fonctionnement réversible. Pour cela, nous allons d'abord rappeler le fonctionnement d'un réfrigérateur. Dans un réfrigérateur, nous fournissons de l'énergie sous forme électrique. Le réfrigérateur reçoit un transfert thermique de la source froide (l'intérieur du réfrigérateur) et effectue un transfert thermique vers la source chaude (l'extérieur du réfrigérateur) où il se réchauffe. Maintenant, passons à la transformation de l'eau en glace. Comme il s'agit d'un changement d'état, cela se fait à pression et température constantes. Pour cela, nous utiliserons la notion de chaleur latente de solidification, qui est l'opposé de la chaleur latente de fusion (l'énergie nécessaire pour faire passer de l'eau solide en eau liquide). Le transfert thermique total reçu par l'eau sera égal à la chaleur latente de fusion multipliée par la masse de l'eau. Cela signifie que le réfrigérateur doit recevoir cette énergie. En d'autres termes, il doit recevoir la quantité d'énergie nécessaire pour solidifier l'eau. Maintenant, nous avons deux quantités : le transfert thermique reçu par le réfrigérateur (QF) et le travail minimal (W) que nous cherchons à déterminer. Selon le premier principe de la thermodynamique, le travail minimal est égal à moins le transfert thermique reçu par le réfrigérateur. Nous pouvons aussi utiliser l'inégalité de Clausius, une application du second principe de la thermodynamique, qui nous dit que moins le transfert thermique de la source chaude divisé par sa température est plus petit que zéro. Finalement, nous obtenons l'expression du travail minimal, qui est égal à moins la masse de l'eau multipliée par la chaleur latente de fusion divisée par la température de la source froide. Il ne reste plus qu'à effectuer les calculs numériques pour obtenir la valeur du travail minimal, soit 23,2 kJ pour transformer 1 kg d'eau liquide en glace. En conclusion, cet exercice nous a permis de comprendre et d'appliquer les concepts de thermodynamique, en particulier ceux liés aux machines thermiques et à la transformation d'état de l'eau. Cela nécessite une compréhension rigoureuse des signes et des équations, mais aussi une application pratique des formules.

Cycle cardiaque

Aujourd'hui, nous allons étudier le cycle cardiaque en tant que cycle thermodynamique. Le cœur joue le rôle d'une pompe dans ce cycle. Le cycle cardiaque est représenté dans un diagramme PV qui décrit l'évolution de la pression et du volume de sang. On nous donne différentes valeurs, telles que VA, VB, VC, VD, PA-P0, PD-P0 et CPA. Le cycle est parcouru dans le sens horaire (A, D, C, B, A) et le cœur agit comme un moteur, fournissant un travail. Pour une transformation réversible, le travail est égal à moins P, D, V, qui est aussi égal à moins l'air du cycle (A). A est positif dans le sens horaire, donc le travail (W) est négatif, confirmant qu'il s'agit bien d'un moteur. En calculant numériquement l'air, nous obtenons 0,72 joules. Pour obtenir la puissance, nous divisons cette énergie par le temps d'un battement (0,86 secondes) et trouvons une puissance de 0,84 watts. Sur une journée, l'énergie fournie par le cœur est de 72 kJ ou 17 kcal, une petite partie de notre consommation énergétique quotidienne. Le cœur joue donc un rôle important mais nécessite une faible quantité d'énergie par rapport à d'autres activités quotidiennes. Ce sujet lie la physique et la biologie.

Rendement de carnot

Aujourd'hui, nous allons parler du rendement de Carnot. En termes simples, le rendement de Carnot est une limite de performance pour une machine thermique telle qu'un moteur, un réfrigérateur ou une pompe à chaleur. Selon le théorème de Carnot, le rendement d'une machine réelle ne peut jamais dépasser celui de Carnot. Le concept clé ici est la réversibilité. En thermodynamique, les systèmes réels présentent souvent des irréversibilités dues à la création d'entropie, ce qui entraîne une perte d'énergie. Cependant, le rendement de Carnot est basé sur l'hypothèse d'un fonctionnement réversible, où aucune entropie n'est créée. Nous avons déjà discuté du rendement de Carnot lors de l'étude des cycles idéaux pour les pompes à chaleur et les moteurs. Pour un moteur, le rendement de Carnot peut être calculé à l'aide de la formule suivante : Rendement = 1 - (Température froide / Température chaude). Il est important de retenir cette formule, car elle est souvent utilisée pour comparer les systèmes au rendement de Carnot. Gardez à l'esprit que cette formule s'applique uniquement aux fonctionnements réversibles. En résumé, le rendement de Carnot représente une limite théorique de performance pour les machines thermiques. Il est basé sur le concept de réversibilité et est calculé en fonction des températures chaude et froide du système.

Relation fondamentale

Aujourd'hui, nous allons examiner la relation fondamentale de la statique des fluides. Cette relation sera utilisée dans tous les problèmes de statique des fluides. Pour cela, nous allons analyser les forces s'appliquant sur un élément de fluide, représenté par un petit cube de volume dv. Les forces qui s'appliquent sur cet élément sont les suivantes : le poids dirigé vers le bas et la résultante des forces de pression exercées par le fluide environnant. La résultante des forces de pression est représentée par F, que nous avons déjà vu comme étant égale à moins grade p dv. Le poids est représenté par ρ dv fois g, où ρ est la masse volumique du fluide. En statique, la somme des forces sur le volume de fluide est nulle. Ainsi, nous obtenons l'équation grade p = ρg.

Atmosphère isotherme

Aujourd'hui, nous allons étudier la statique des fluides dans l'atmosphère isotherme. Ce modèle est utilisé couramment en mécanique des fluides. L'objectif est de déterminer la distribution de pression dans l'atmosphère en supposant qu'elle a une température constante partout. Bien que cette hypothèse ne soit pas tout à fait exacte, elle constitue une bonne approximation et est souvent utilisée dans les exercices et les concours. Pour commencer, nous devons déterminer la position de l'axe z, qui est choisi dirigé vers le haut. Il est important de faire ce choix correctement, car il influence la projection de la relation fondamentale de la statique des fluides. Dans notre cas, cette relation est donnée par dp/dz = -ρg, où ρ représente la densité et g est le vecteur gravité. Nous avons une équation différentielle en z pour décrire le champ de pression. Cependant, la densité ρ n'est pas constante et nous devons l'éliminer. Pour cela, nous utilisons la loi des gaz parfaits, que nous réécrivons en termes de densité (ρ) plutôt que de volume (V). En réinjectant cette expression dans notre équation différentielle, nous obtenons dp/dz + p(ρM)/(rtg) = 0. Dans cette équation, tout ce qui est en bleu est une constante car nous considérons l'atmosphère isotherme. Nous définissons donc cette constante comme étant égale à 1/h. En résolvant cette équation homogène, nous obtenons une expression pour la pression, p(z) = p0 * exp(-z/h), où p0 est une constante. Cette équation est souvent utilisée pour décrire la pression dans l'atmosphère selon le modèle isotherme. Dans l'atmosphère terrestre, la valeur typique de h est d'environ 8 km. Il est donc important de retenir que la pression varie exponentiellement avec l'altitude selon ce modèle. J'espère que ce résumé vous a été utile. Les points clés à retenir sont de faire attention au choix de l'axe z et d'éliminer correctement les grandeurs dans l'équation différentielle, comme nous l'avons fait avec la densité ρ.