Cours d'apprentissage en ligne

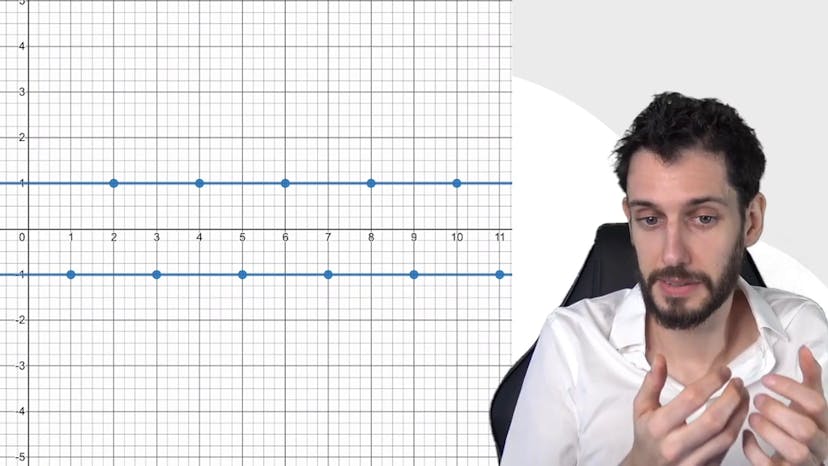
Unicité et Divergence

La convergence se réfère à la limite finie d'une suite. Lorsque vous avez une limite finie, elle est unique, ce qui signifie qu'une suite ne peut tendre vers deux valeurs différentes. Cependant, il est important de noter que le fait d'être divergent, c'est-à-dire de ne pas être convergent, ne signifie pas nécessairement tendre vers l'infini positif ou négatif. Il existe des cas où une suite peut osciller sans tendre vers une limite finie. Par exemple, la suite (-1)^(n) oscille entre -1 et 1 sans converger vers l'un ou l'autre. Bien que certains termes de la suite puissent sembler converger vers 1 ou -1, dans son ensemble, cette suite n'a pas de limite. Il est possible d'extraire des sous-suites pour lesquelles la convergence est observable, mais cela dépasse le cadre du programme scolaire. En résumé, la convergence d'une suite vers une limite finie est unique, mais il est également possible d'avoir des suites divergentes qui n'oscillent pas vers l'infini. Si vous avez besoin de plus de détails, n'hésitez pas à consulter la FAQ ou à discuter avec nous. À bientôt !

Limites de référence et opérations

Ce cours traite de la convergence et de la divergence des suites. Il aborde les outils pratiques à connaître tels que les puissances de n qui tendent vers l'infini, les puissances négatives de n qui tendent vers zéro, et les opérations sur différentes suites. Il est important de connaître les formes indéterminées, qui sont des cas où il n'y a pas de règle prédéterminée et qui nécessitent une approche cas par cas. Les formes indéterminées comprennent la somme, le produit et le quotient de deux suites qui tendent respectivement vers l'infini, zéro et l'infini ou zéro. Il est essentiel de mémoriser ces formes indéterminées et de les appliquer dans les exercices. En résumé, il est recommandé d'apprendre les tables par cœur et de se familiariser avec les différentes formes indéterminées.

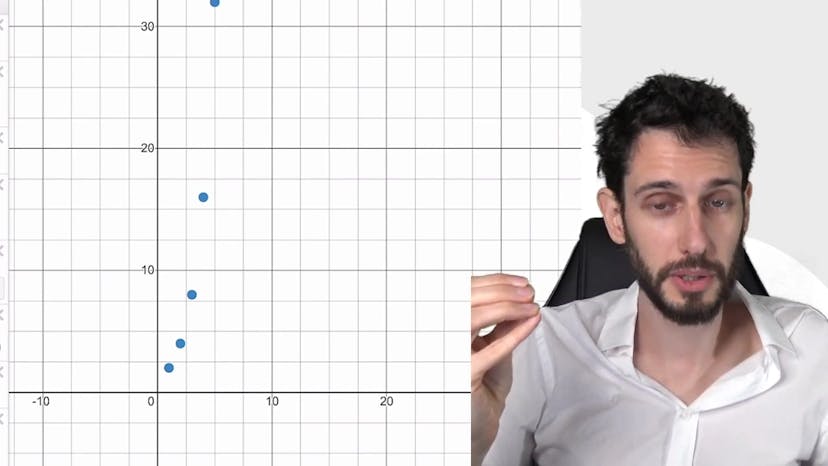
Suites géométriques - illustration

Dans cette vidéo, nous abordons le sujet des suites géométriques et leurs différents comportements en fonction de la valeur de la raison (Q). Tout d'abord, lorsque Q est supérieur à 1, on nous dit que Q à la puissance n tend vers l'infini. Cela est illustré en prenant l'exemple de Q égal à 3, où chaque terme de la suite augmente de plus en plus. Ce comportement peut être démontré à l'aide de l'inégalité de Bernoulli. Ensuite, lorsqu'on a une raison entre -1 et 1 (pour le cas positif), on observe que la suite se rapproche de plus en plus de zéro. Par exemple, avec Q égal à 0,5, chaque terme de la suite diminue de moitié à chaque étape, et finit par converger vers zéro. Ce comportement est intuitive, car on enlève un petit bout à chaque fois. Pour le cas négatif, où Q est strictement inférieur à -1, on observe un comportement plus complexe. La suite oscille entre des valeurs positives et négatives, mais converge tout de même vers zéro. Par exemple, avec Q égal à -0,7, on voit que certains termes sont positifs tandis que d'autres sont négatifs, mais l'ensemble de la suite se rapproche de zéro. Finalement, le cas où Q est égal à 1 est trivial, car tous les termes de la suite sont égaux à 1. En résumé, lorsque la raison est proche de zéro (-1 < Q < 1), la suite converge vers zéro, soit en oscillant, soit non. Lorsque la raison est supérieure à 1 ou inférieure à -1, la suite s'écarte de zéro, soit en tendant vers l'infini, soit d'une manière plus complexe en s'écartant des deux côtés à la fois.

Suites géométriques : démo

Dans cette vidéo, nous démontrons les intuitions sur la limite des suites géométriques pour plusieurs cas. Si q est plus grand que 1, nous utilisons l'inégalité de Bernoulli et le terrain de comparaison pour montrer que la limite de q puissance n tend vers plus infini. Pour le cas où q est entre 0 et 1, nous posons p égal à 1 sur q et appliquons le résultat précédent pour montrer que p plus s enseigne tend vers plus infini et donc que q plus s enseigne tend vers 0. Enfin, pour le cas où q est entre moins 1 et 0, nous utilisons le théorème des gendarmes pour montrer que q puissance n tend vers 0. La démonstration est à savoir par cœur dans le programme.

Calcul d'expressions 1

Ce cours explique comment calculer les sinus et cosinus pour des expressions qui dépendent de n en utilisant le cercle trigonométrique. Le cercle trigo est une manière de voir les angles en associant un angle à la longueur de cercle qu'il peut parcourir. Les longueurs d'arc associées à un angle ont la même valeur de cosinus-sinus et peuvent être associées à une certaine valeur π ou un nombre de cercles en plus. Les valeurs de cosinus et sinus pour les expressions 2nπ, 2n+1π et nπ sont déduites. Le résultat pour nπ dépend de n, avec un sinus de 0 et un cosinus de -1 ou 1 si n est pair ou impair respectivement. Enfin, une expression complexe est simplifiée pour trouver le cosinus et le sinus pour le point correspondant. Il est important de retenir que moins 1 puissance n correspond à 1 si n est pair et à -1 si n est impair pour nπ.

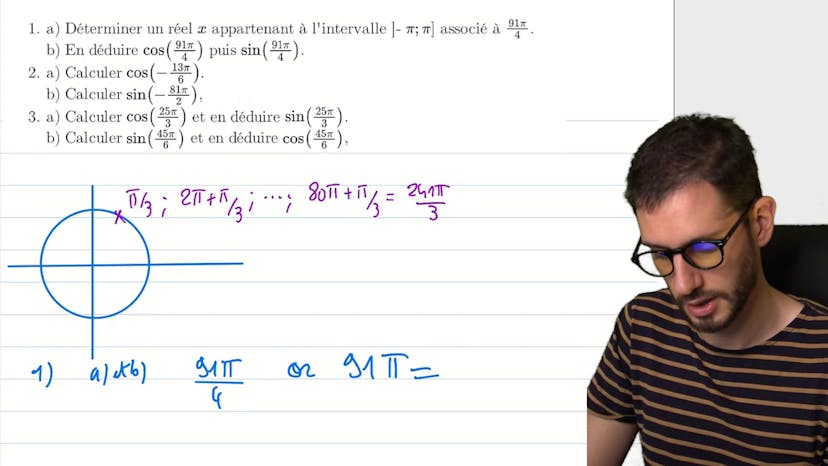
Calcul d'expressions 2

Apprendre les valeurs trigonométriques peut être simplifié en trouvant des valeurs équivalentes plus courantes. Par exemple, 241pi/3 peut être simplifié en pi/3 pour trouver les valeurs de cosinus et sinus. Pour trouver les valeurs pour 91pi/4, vous pouvez retirer des paquets de 2pi et exprimer 91pi/4 comme 10 paquets de 2pi plus 3pi/4. Les valeurs de cosinus et sinus pour 91pi/4 sont les mêmes que pour pi/4, mais avec des signes différents. Les questions 2a, b et 3a, b utilisent la même méthode.

Points sur le cercle trigo

Dans cet exercice sur le cercle trigonométrique, on doit placer des points astucieusement. Le point A associé au réel pi sur 3 est placé sur le cercle trigo. Ensuite, le point B symétrique de A par rapport à l'axe des abscisses est tracé. Les réels associés à ces points dans l'intervalle 0 de pi et dans l'intervalle moins pi pi sont demandés. Il y a une faute de français car ils veulent dire le réel associé à ce point dans chaque intervalle, pas les réels associés. Le nombre associé à A est pi sur 3, à B c'est 5 pi sur 3, et à C c'est 2 pi sur 3. Enfin, le point D symétrique de A par rapport à O est placé et le réel associé à ce point est 4 pi sur 3 entre 0 et 2 pi, et moins 2 pi sur 3 entre moins pi et pi. Il faut comprendre qu'on peut parcourir plusieurs tours et qu'un seul point du cercle peut représenter plusieurs nombres.

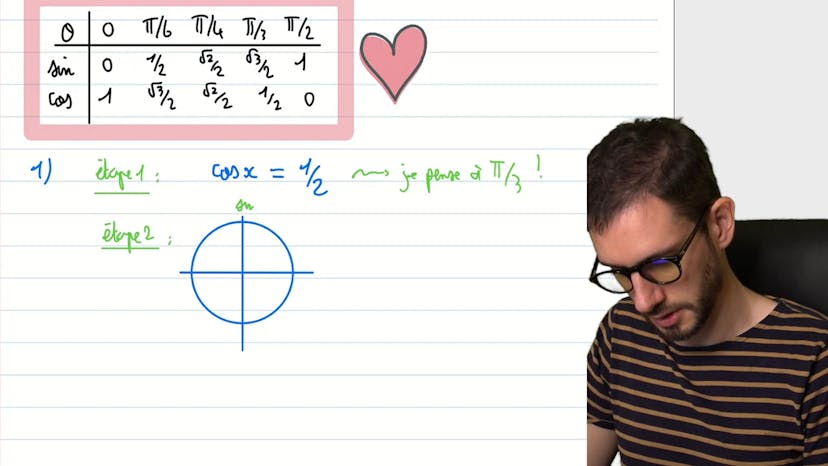
Equations trigos simples

La vidéo explique comment résoudre des équations trigonométriques simples en utilisant le cercle trigonométrique et le tableau des valeurs de sine et cosine. La première étape consiste à identifier la valeur classique à laquelle on peut se rapporter dans le problème. La deuxième étape consiste à tracer le cercle trigonométrique pour trouver les points où l'équation est vérifiée. Il est important de comprendre la contrainte de l'intervalle et de trouver les angles solutions dans cette plage. La vidéo illustre cet exemple pour résoudre 2cos(x) = 1 dans l'intervalle [0, 2π] avec les solutions x=π/3 et x=5π/3 et pour résoudre 2sin(x) = -1 avec les solutions x=7π/6 et x=11π/6 dans cet intervalle.

Inéquations trigos simples

Ce cours explique comment résoudre des inéquations en utilisant un tableau de valeurs de base. Le premier exemple montre comment réécrire une inéquation en utilisant le cosinus et la racine de 2. En traçant un cercle trigo et en utilisant le point pi sur 4, l'élève peut identifier les angles pour lesquels le cosinus est inférieur à pi sur 4, en excluant les points de l'axe des abscisses. L'ensemble des angles est entre moins pi et pi, en incluant moins pi sur 4 exclu et pi sur 4 exclu. Le deuxième exemple utilise la racine de 2 sinus x et se réécrit en utilisant la racine de 6, qui peut être simplifiée, et en utilisant le sinus. Le cercle trigo est tracé sur l'axe vertical, en utilisant le point pi sur 3. L'ensemble des angles avec un sinus supérieur à racine de 3 sur 2 est entre moins pi et pi et inclus pi sur 3 et 2 pi sur 3. En résumé, pour résoudre une inéquation, il faut transformer l'équation pour utiliser le tableau de valeurs, tracer un cercle trigo, puis lire les angles correspondants en parcourant l'ensemble donné.

Equation trigo où poser X=sinx

Dans ce cours, on apprend à résoudre une équation trigonométrique qui inclut cos et sin, ainsi que des termes cos² et sin². Pour simplifier l'équation, on utilise l'identité fondamentale de la trigonométrie pour remplacer cos² par 1-sin². Ensuite, on pose un grand X pour résoudre l'équation de degré 2 qui apparaît. Finalement, on revient à la trigonométrie pour trouver les solutions de l'équation d'origine en fonction de X. Les solutions en fonction de X forment un cercle trigo et l'ensemble des solutions réelles est obtenu en trouvant quand le sinus vaut 1.

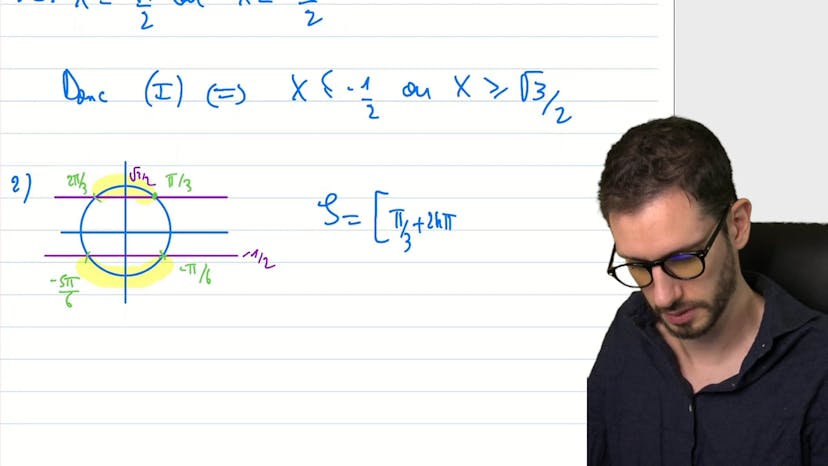
Inéquation trigo où poser X=sinx

Dans cette leçon de mathématiques, nous avons une équation avec seulement du sinus, donc pas besoin de faire un changement de variable. Nous résolvons l'équation en posant "X = sin(x)" et en trouvant les racines à partir de cela. Ensuite, nous utilisons une astuce pour résoudre l'inéquation qui nous est donnée. Nous rappelons également la méthode X2-XS+P pour trouver les racines d'une équation à deux degrés. Finalement, nous utilisons une méthode trigo pour trouver l'ensemble des solutions.