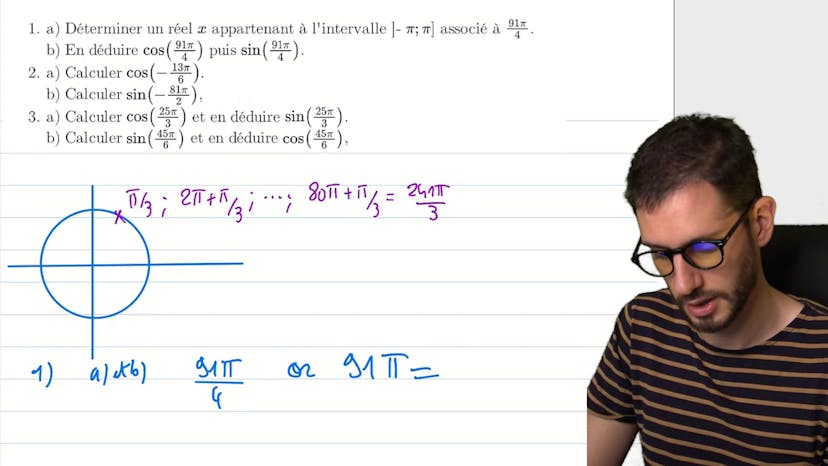Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Calcul d'expressions 1
Ce cours explique comment calculer les sinus et cosinus pour des expressions qui dépendent de n en utilisant le cercle trigonométrique. Le cercle trigo est une manière de voir les angles en associant un angle à la longueur de cercle qu'il peut parcourir. Les longueurs d'arc associées à un angle ont la même valeur de cosinus-sinus et peuvent être associées à une certaine valeur π ou un nombre de cercles en plus. Les valeurs de cosinus et sinus pour les expressions 2nπ, 2n+1π et nπ sont déduites. Le résultat pour nπ dépend de n, avec un sinus de 0 et un cosinus de -1 ou 1 si n est pair ou impair respectivement. Enfin, une expression complexe est simplifiée pour trouver le cosinus et le sinus pour le point correspondant. Il est important de retenir que moins 1 puissance n correspond à 1 si n est pair et à -1 si n est impair pour nπ.