 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Prépa Examens
Prépa Examens Révisions Maths lycée
Révisions Maths lycée
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Prépa Examens
Prépa Examens Révisions Maths lycée
Révisions Maths lycée
Maths
Analyse
MPSI/PCSI
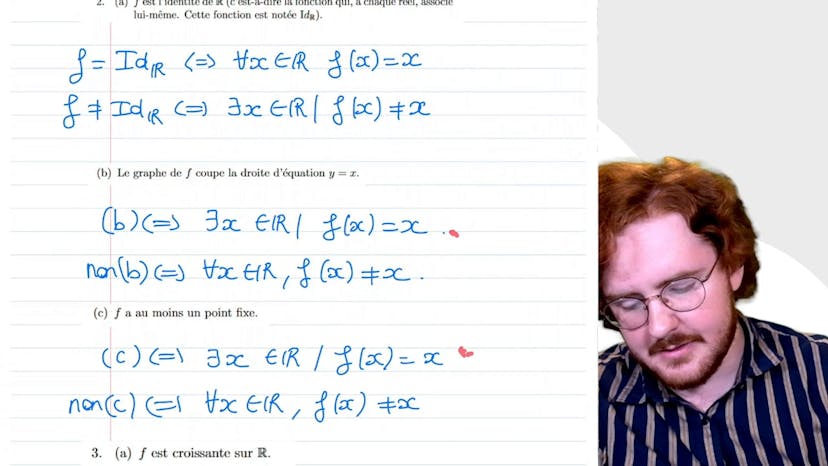
Utiliser les quantificateurs
Dans cette vidéo, Paul explique comment traduire des phrases logiques en français en utilisant des quantificateurs mathématiques. Il utilise des exemples avec une fonction f de r à R et explique comment exprimer ces phrases à l'aide de quantificateurs et leur négation. Les exemples incluent des questions sur l'unicité de solutions, l'existence de points fixes, la croissance/decrémentation de la fonction et l'annulation de la fonction sur R. Paul souligne qu'il y a différentes façons de décrire la même chose avec des quantificateurs et il explique comment prendre la négation d'une implication en utilisant la logique "a et non b". En somme, cette vidéo est un guide pour comprendre et utiliser correctement les quantificateurs mathématiques pour traduire des phrases logiques en français.
Maths
Analyse
MPSI/PCSI

Ecrire la négation
Dans cette vidéo, on apprend comment traduire des assertions en français en des assertions logiques avec des quantificateurs, cet exercice se concentre sur des suites réelles UN définies sur N. Pour exprimer que l'assertion "la suite UN est majorée", il faut dire qu'il existe un nombre M appartenant à R tel que, pour tout N appartenant à N, UN est inférieur ou égal à M. En négatif, il faut dire que, quel que soit M appartenant à R, il y a au moins un rang N tel que UN est supérieur à M. Pour l'assertion "la suite UN est bornée", elle est équivalente à dire qu'il existe un petit M et un grand M appartenant à R² tels que, pour tout N appartenant à N, UN est compris entre petit M et grand M. En négatif, il faut dire soit qu'elle est non bornée car il existe un rang N tel que UN est strictement inférieur à petit M pour tout M appartenant à R, soit qu'elle est non bornée car il existe un rang N à partir duquel UN est strictement supérieur ou égal à tout M appartenant à R. Pour l'assertion "la suite UN est décroissante", il suffit de dire que, pour tout N appartenant à N, UN est inférieur à UN plus 1. En négatif, il faut dire qu'il existe un rang N tel que UN est supérieur à UN plus 1. Enfin, pour l'assertion "la suite UN est monotone", elle est soit croissante, soit décroissante, il faut donc utiliser le quantificateur "quel que soit" avec chaque affirmation.
Maths
Analyse
MPSI/PCSI

Equivalence et implication
Dans ce cours, Paul explique comment utiliser les implications et les équivalences en résolvant des problèmes logiques. Il donne trois exemples de problèmes et explique comment déterminer si l'équivalence ou l'implication est réciproque ou directe. Le premier problème concerne x appartenant à R tel que x² égale à 4, Paul parvient à prouver que l'implication est seulement dans le sens retour. Le deuxième problème concerne z qui est un complexe et si z est égal à son conjugué, est-ce que z appartient à R ? Paul parvient à prouver que l'équivalence est vraie. Le troisième problème concerne x appartenant à R tel que x égale à pi et e2i x égale à 1. Paul parvient à prouver que l'implication est seulement dans le sens direct.
Maths
Analyse
MPSI/PCSI

Raisonner par l'absurde
Dans cette vidéo, Paul démontre que si a et b sont deux entiers tels que a plus b racine de 2 égal à 0, alors a = b = 0. Il utilise la logique par l'absurde en supposant que a ou b est différent de 0 et montre que cela mène à une contradiction. Ensuite, il démontre que si m plus n racine de 2 égal à p plus q racine de 2 pour des entiers m, n, p et q, alors m = p et n = q. Il utilise le résultat de la première partie et arrive à cette conclusion en rassemblant les termes et en montrant que n moins p et n moins q sont égaux à 0. Cette vidéo est utile pour comprendre la logique impliquée dans les preuves mathématiques.
Maths
Analyse
MPSI/PCSI
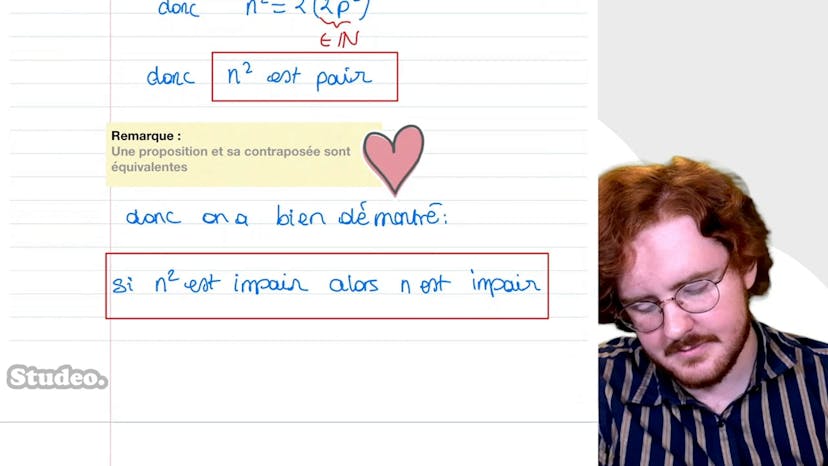
Raisonner par contraposée
Dans ce cours sur la démonstration par la contraposée, Paul explique comment démontrer une proposition en utilisant sa contraposée qui consiste à inverser la relation et les termes. Pour illustrer cela, il prend l'exemple de la proposition suivante: si n² est impair, alors n est impair. En utilisant la contraposée, il dit que si n est pair, alors n² est pair. Ensuite, il démontre cette contraposée en expliquant qu'un nombre pair peut être représenté comme 2p et donc n² sera égal à 2 facteurs de 2p², ce qui est pair. Il conclut en expliquant que quand la contraposée est plus facile à démontrer, on peut l'utiliser pour démontrer la proposition initiale.
Maths
Analyse
MPSI/PCSI
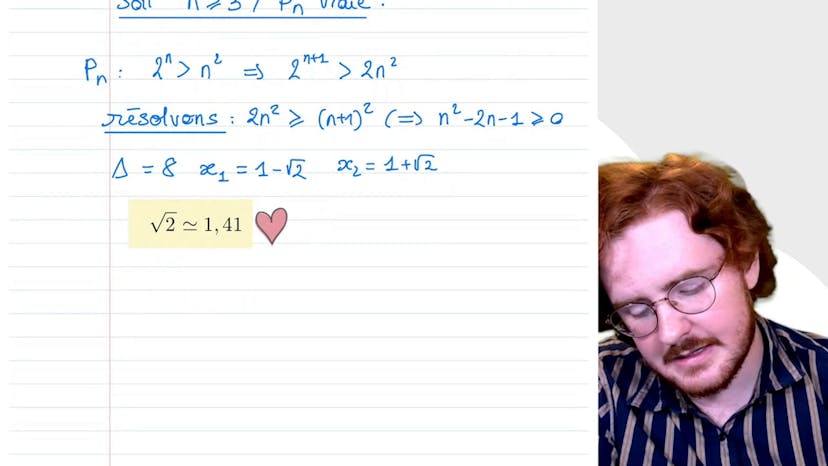
Raisonner par récurrence
Paul explique comment travailler le raisonnement par récurrence en démontrant la propriété pn ≥ n² pour n appartenant à n. Pour prouver la récurrence, il utilise une implication qui montre que si pn est vraie, alors pn plus 1 est également vraie pour n supérieur ou égal à 3. Il démontre ensuite l'initialisation pour n égal à 3, qui se révèle fausse en testant la propriété. En testant les valeurs supérieures de n, il trouve que pour n égal à 5, la propriété est vraie. Ainsi, il conclut que la propriété est vraie pour tout n supérieur égal à 3, et que le rang cherché est 5.
Maths
Analyse
MPSI/PCSI

La récurrence forte
Dans ce cours, Paul explique comment utiliser le raisonnement par récurrence pour démontrer une relation de récurrence forte. Il donne l'exemple d'une suite u1 définie par u1 = 3 et la somme des n premiers termes de la suite divisée par deux fois n pour toute n. On veut démontrer que pour toute n, u1 est égale à 3n. Paul définit une propriété pn (récurrence forte) pour montrer que tous les uk sont égaux à 3k et pas seulement u1 = 3n. Il effectue ensuite une initialisation (n = 1) et démontre l'hérédité pour n + 1 en deux cas: k appartient à 1 à n et k = n + 1. Lorsque k appartient à 1 à n, la propriété est prouvée car on sait que tous les uk sont égaux à 3k grâce à pn. Ensuite, en remplacant les ui par 3j, on obtient la somme des j allant de 0 à n, qui est égale à n(n+1)/2. Après avoir simplifié, on obtient 3n, ce qui prouve que pn + 1 est vrai. Ainsi, pn est vrai pour tout n et un est égal à 3n pour tout n.
Maths
Analyse
MPSI/PCSI
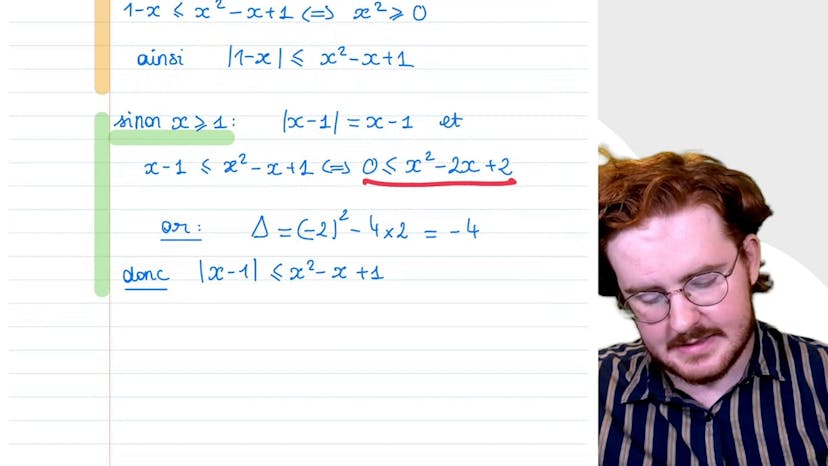
La disjonction de cas
Dans cette vidéo, Paul explique le raisonnement par disjonction de cas avec pour exemple une équation à démontrer. Il montre comment enlever la valeur absolue de la variable x en divisant les cas en deux parties: si x est inférieur à 1 ou si x est supérieur ou égal à 1. Dans le premier cas, il développe la formule pour montrer que l'inégalité est vraie, et dans le deuxième cas, il montre que le polynôme est toujours positif, ce qui prouve également que l'inégalité est vraie. Finalement, il démontre que pour tout x réel, la valeur absolue de x-1 est inférieure ou égale à x²-x plus 1.
Maths
Analyse
MPSI/PCSI

Analyse-Synthèse
Dans cette vidéo, Paul explique comment résoudre un exercice en utilisant un raisonnement d'analyse synthèse en SEO friendly. L'exercice consiste à déterminer les réels x tels que racine de 2-x est égale à x. Pour commencer, on fait une analyse en supposant qu'il existe un x tel que l'énoncé soit vrai. On trouve que x doit être supérieur à 0 et qu'il est égal à 1 si on résout le polynôme obtenu. Cela prouve l'unicité de x, mais pas son existence. Pour prouver son existence, on vérifie si la relation fonctionne pour x=1, ce qui est le cas. Ainsi, on trouve que x est égal à 1 et est l'unique réelle vérifiant la condition.
Maths
Analyse
MPSI/PCSI
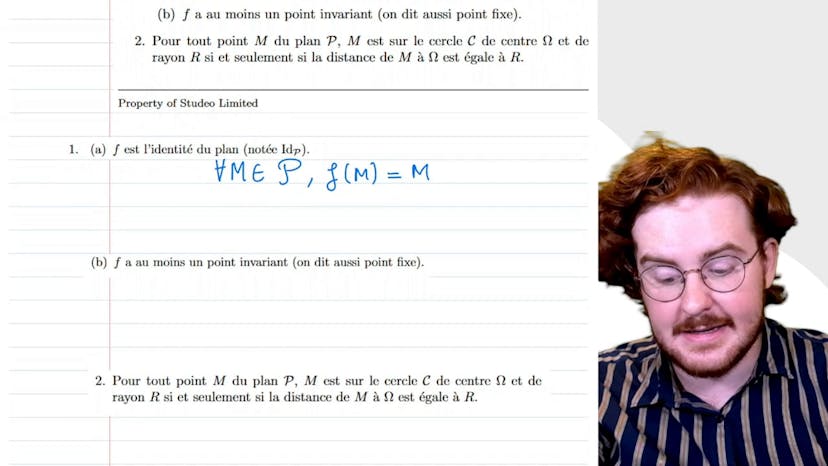
Quantificateurs un peu chauds
Dans cette vidéo, Paul explique l'importance des quantificateurs en mathématiques en utilisant l'exemple d'une fonction f du plan dans lui-même. Il explique que le plan P est un ensemble au même titre que R et que cela ne change rien quant aux quantificateurs utilisés. Il traduit ensuite l'affirmation que f est l'identité du plan en utilisant des quantificateurs, et explique comment on peut également traduire la négation de cette affirmation. Enfin, il explique comment traduire l'affirmation que pour tout point M du plan P, M est sur un cercle C de centre oméga et de rayon R si et seulement si la distance de M à oméga est égale à R, en utilisant des quantificateurs.
Maths
Analyse
MPSI/PCSI

Vrai ou Faux corsé
Paul explique dans cette vidéo un exercice de logique consistant à déterminer si une affirmation est vraie ou fausse. Pour cela, il faut savoir traduire les termes "suffit", "faux", "nécessaire" et "suffisant" en termes de quantificateurs implicatifs ou d'équivalences. Les exemples d'exercices montrent comment appliquer cette astuce pour déterminer la vérité des affirmations. En résumé, pour réussir ce type d'exercice, il est important de comprendre les relations entre les termes "il suffit", "il faut", "il est nécessaire" et de les traduire correctement en termes implicatifs ou équivalents.
Maths
Analyse
MPSI/PCSI
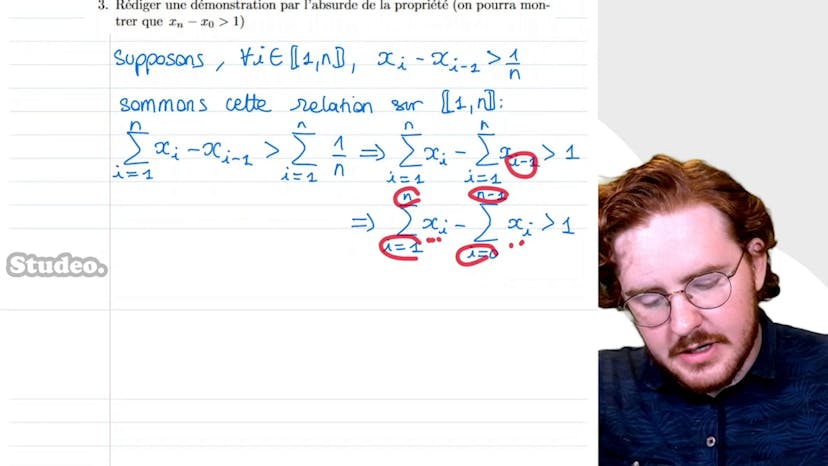
Absurde et principe des tiroirs
Le cours explique le raisonnement par l'absurde pour prouver une propriété mathématique. La propriété à démontrer impose la présence d'au moins deux réels x_i et x_j (parmi un ensemble de x_0, x_1, ... x_n) tels que la distance entre eux est inférieure ou égale à 1/n. Pour commencer, on écrit la propriété sous forme de quantificateurs pour pouvoir facilement écrire sa négation. Ensuite, pour démontrer la propriété, on suppose sa négation et on cherche à obtenir une contradiction. On utilise la somme télescopique pour montrer que x_n - x_0 est supérieur ou égal à 1, ce qui est une contradiction puisque x_n et x_0 sont dans [0,1]. Enfin, on démontre la propriété autrement en utilisant le principe des tiroirs : on divise [0,1] en n segments de même longueur et on range les x_i dans ces segments. Comme il y a n+1 x_i et seulement n segments, il doit y avoir au moins deux x_i dans un même segment, ce qui implique que leur distance est inférieure ou égale à 1/n.


