Cours d'apprentissage en ligne

Analyse de relevé expérimental

Dans cette vidéo, Matisse de Studio analyse un relevé expérimental d'un circuit composé d'une bobine, d'un condensateur et d'un générateur imposant un échelon de tension. Il cherche à déterminer la hauteur de l'échelon de tension, la nutance et la capacité. Il identifie les informations disponibles dans la courbe, y compris un temps caractéristique, une pseudo-période et différentes amplitudes. Il modélise ensuite le circuit en incluant une résistance interne du générateur et résout l'équation différentielle pour obtenir les paramètres RLC série habituels. À partir de là, il peut extraire la nutance et la capacité en utilisant √1/2² et 4Pi²/pseudo-période². Enfin, il utilise les conditions initiales pour déterminer la hauteur de l'échelon de tension, en obtenant un résultat de -5V. La vidéo montre une démarche pratique pour analyser les relevés expérimentaux et manipuler les équations pour obtenir les informations recherchées.

Equation différentielle du RLC série

Dans cette vidéo, Mathis de Studio explique comment établir l'équation différentielle du RLC série, en étudiant la tension au bord du condensateur et le courant qui passe. Il utilise la loi des mailles pour obtenir l'équation de base et la relation courant-tension pour l'exprimer en fonction de UC. L'équation ainsi obtenue est LC D2 UC sur DT2 plus RC D2 UC sur DT plus UC égale à 0, ce qui correspond à une dérivée d'ordre 2. Pour la mettre sous une forme normalisée, il faut identifier omega 0 et Q, qui sont respectivement la pulsation propre et le facteur de qualité associé au circuit. Les élèves ont parfois du mal à comprendre ces grandeurs, mais Mathis prévoit de faire plusieurs exercices pour les aider à mieux les cerner.

RLC série

Dans cette vidéo, Matisse de Studio réalise une étude énergétique du circuit RLC série afin d'expliquer les transferts de puissance entre les différents dipôles. Pour cela, tous les dipôles vont intervenir, notamment le générateur, le condensateur, la bobine et la résistance. Pour déterminer I, on utilise la relation courant-tension pour le condensateur, qui fournit une expression longue pour I de t. On peut ensuite déterminer les variations d'énergie pour le condensateur et pour la bobine à partir des instants initiaux et finaux, ce qui permet d'accumuler une énergie de 1,5 CE² pour le condensateur et aucune pour la bobine. En ce qui concerne le générateur, la puissance fournie en électricité est E fois I2t, tandis que l'énergie fournie par le condensateur sur tout le cycle est CE². Enfin, la résolution classique permet de déterminer que l'énergie dissipée par effet joule est égale à ½ CE². Au final, le générateur fournit une énergie CE², qui est répartie entre les différents dipôles de manière équitable, avec ½ de CE² pour le condensateur et ½ de CE² pour l'effet joule. Cette étude énergétique du circuit RLC série est un exercice classique en électricité.

Portrait de phase d'un oscillateur

Dans cette vidéo, Matisse de Studio étudie le portrait de phase d'un oscillateur qui est représenté sur un graphe avec une grandeur x et sa dérivée v en ordonnée. Deux portraits de phase sont présentés pour un micro oscillateur mécanique plongé dans deux fluides différents. Matisse nous guide à travers les étapes pour orienter les portraits de phase, indiquer le type de régime qu'ils décrivent et construire le chronogramme x2t associé à chaque portrait de phase. Les portraits de phase orientés dans le sens horaire décrivent un régime pseudo-périotique avec des oscillations nombreuses et amorties, tandis que l'autre décrit un régime apériotique sans oscillation autour de la position d'équilibre. Les vitesses et les déplacements considérés sont en millimètres et les évolutions sont de l'ordre de grandeur de la seconde. Le portrait de phase est un outil puissant pour tirer des informations intéressantes sur l'évolution d'un système électronique ou mécanique.

Résolution de l'équation différentielle du RLC série

Dans cette vidéo, on résout l'équation différentielle associée au RLC série. On étudie la tension UC au banc du condensateur dans un circuit RLC série. On détermine les conditions initiales vérifiées par UC et sa dérivée temporelle. Ensuite, on résout l'équation d'oscillateur amorti vérifiée par UC. On distingue les trois types de régime : apériodique, critique et pseudo-périodique. On détermine les racines de l'équation caractéristique et on trouve la solution homogène pour chaque régime. Ensuite, on cherche une solution particulière et on somme les deux solutions pour résoudre les constantes. On obtient finalement la solution de l'équation globale. La résolution de cette équation différentielle linéaire d'ordre 2 est importante pour comprendre les caractéristiques d'un circuit RLC série.

Association de dipôles

Dans cette vidéo, Mathilde Studio explique comment associer des dipôles de manière complexe. Elle commence par montrer un bout de circuit composé d'une résistance et d'un condensateur en série. Elle explique ensuite comment déterminer l'impédance équivalente aux dipôles en régime sinusoidal, ainsi que sa résistance et sa réactance. Elle souligne que l'impédance équivalente permet d'identifier des dipôles à des résistances, tout comme les associations de résistances. Elle montre comment l'impédance des dipôles en série s'ajoutent pour donner la somme des impédances. Elle déduit la nature des dipôles ainsi formés, qui comportent une partie résistive et une partie capacitive. Elle explique comment relier la tension complexe E qui s'applique à l'ensemble des dipôles au courant complexe I qui les traverse, et comment obtenir des signaux en quadrature de phase. Elle détermine finalement l'expression réelle de E pour I², qui vaut I0 sin ωt, en appliquant la loi d'Ohm en complexe et en utilisant une manipulation qui consiste à passer du signal complexe au signal réel en intégrant ou en dérivant. Elle insiste sur l'importance de cette transformation en complexe pour simplifier les calculs.

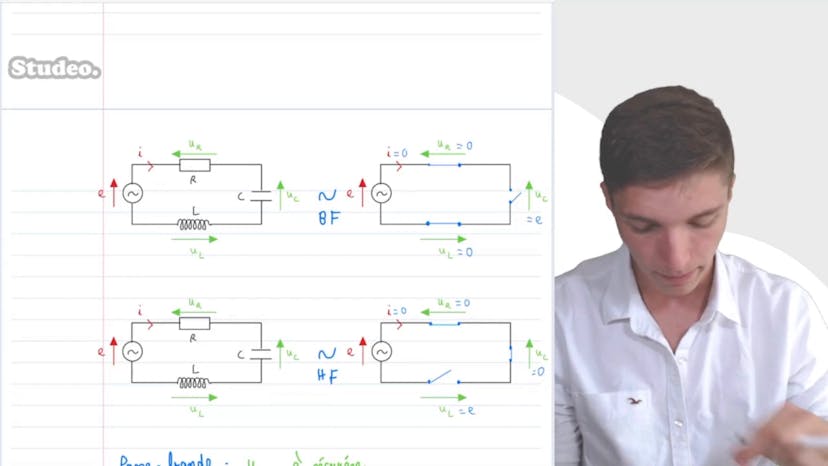
Créer un filtre

Dans cette vidéo, Matisse de Studio explique comment créer un filtre à partir d'un circuit RLC série. Pour choisir la tension de sortie et réaliser un filtre passe-vente, il faut analyser le comportement asymptotique du filtre en basses et hautes fréquences. Les impédances complexes des dipôles (bobine et condensateur) déterminent si l'interrupteur est ouvert ou fermé et si la tension est récupérée aux bandes de résistance, aux bandes du condensateur ou aux bandes de la bobine. Les filtres peuvent être utilisés dans différents domaines industriels, tels que l'imagerie ou l'étude sonore, pour réaliser des filtres passe-bandes, passe-haut et passe-bas.

Filtre passe-haut RLC

Bonjour à tous, dans cette vidéo, nous allons réaliser un filtre passe-eau pour un circuit RLC série. Pour cela, nous devons justifier que ce filtre est bien passe-eau, définir sa pulsation caractéristique ω0 et son facteur de qualité Q. Pour déterminer le caractère passe-eau du circuit, nous devons mener une étude asymptotique. Dans une précédente vidéo, nous avons démontré que le circuit RLC série est équivalent à un circuit basse fréquence et un circuit haute fréquence. Ainsi, pour réaliser un filtre passe-eau, nous devons sélectionner la tension aux bornes de la bobine, car elle filtre les basses fréquences. La pulsation propre et le facteur de qualité du filtre peuvent être déterminés en utilisant la méthode classique pour un circuit RLC série. Nous devons ensuite exprimer la fonction de transfert du filtre sous la forme h = jqx / (1 + jqx - 1/x). Pour cela, nous utilisons le diviseur de tension avec les impédances complexes. En normalisant la fonction de transfert, nous obtenons l'équation demandée. Ensuite, nous devons déterminer les pentes des asymptotes du diagramme de Bode-Anguin, en supposant que le facteur de qualité du circuit n'est pas raisonnable. Pour calculer le module de la fonction de transfert, nous utilisons l'expression qx / (1 + q²x² - 1/x²) et déterminons le terme dominant en basse fréquence et en haute fréquence. En basse fréquence, la pente est de 40 décibels par décade et en haute fréquence, la pente est de 0. En traçant le diagramme de Bode en fonction du logarithme de la pulsation, nous pouvons esquisser l'allure du filtre passe-eau. Enfin, nous étudions si le filtre peut avoir un comportement dérivateur ou intégrateur. Cela se remarque sur le diagramme de Bode par une pente de plus ou moins 20 décibels par décade. Dans ce cas, le filtre n'a pas de comportement dérivateur ou intégrateur. Le diagramme de Bode est donc un outil très utile pour visualiser rapidement les caractéristiques d'un filtre. Merci pour cette étude du filtre passe-eau d'un RLC et à bientôt.

Filtre RL série

Dans cette vidéo, on étudie un filtre RL série qui permet de réaliser un filtre passe-bas du premier ordre. En effet, la bobine a une impédance complexe qui tend vers zéro en basse fréquence et qui s'oppose au courant en haute fréquence, ce qui coupe les basses fréquences. La fonction de transfert du filtre est H = H0Jω/ωc / (1+Jω/ωc), où ωc est la pulsation de coupure du filtre. Les pentes des asymptotes en gain dans les limites hautes et basses fréquences sont respectivement de plus 20 dB par décade et de 0, ce qui caractérise un circuit du premier ordre avec une différence de 20 dB entre les deux asymptotes. Les filtres du second ordre ont une différence de 40 dB entre les deux asymptotes. Enfin, la méthode de vérification supplémentaire permet de confirmer que ce circuit est du premier ordre.

Signal non harmonique

Dans cette vidéo, on apprend à filtrer un signal non harmonique en utilisant la transformation de Fourier et une fonction de transfert harmonique. Le signal d'entrée est une forme d'onde créneau et sa représentation temporelle est donnée en série de Fourier. Le filtre utilisé est un filtre passe-bas dont la fonction de transfert est donnée en jω. En utilisant l'analyse complexe et la formule de filtrage linéaire, on détermine l'expression du signal de sortie en fonction de la fonction de transfert et du signal d'entrée. Il est important de comprendre cette résolution pour maîtriser l'enjeu du filtrage linéaire en électricité.

Battements

Dans cette vidéo, on étudie le phénomène de battement en se basant sur un relevé expérimental représentant une somme de deux signaux sinusoïdaux. La représentation de Fresnel, qui utilise des vecteurs pour représenter l'amplitude et la phase des signaux, permet de comprendre le phénomène. La fréquence de battement est déterminée à partir de la période d'oscillation et la période de battement. Les différences entre les phases des signaux déterminent l'amplitude du signal résultant. Grâce à l'analyse des relevés expérimentaux, les fréquences et amplitudes des signaux sont déterminées. La représentation de Fresnel est un outil utile pour comprendre le phénomène de battement.