Cours d'apprentissage en ligne

Bruit sur un chantier

Dans cette vidéo, on évalue le bruit d'un chantier pour savoir si cela peut causer des dommages auditifs à un ouvrier. On utilise l'expression de la dilution sphérique pour déterminer la puissance sonore émise par l'engin à différentes distances. On utilise aussi une formule pour calculer le niveau d'intensité sonore en décibels. Le seuil de danger pour le système auditif est de 85 dB. On montre l'importance de porter des casques anti-bruit, qui ont une atténuation d'au moins 20 dB, afin de protéger l'ouïe. En se déplaçant à 10 mètres, ou en portant un casque anti-bruit à un mètre, l'ouvrier est protégé et le niveau d'intensité sonore est en dessous du seuil de danger.

Voiture et effet Doppler

Aujourd'hui, dans cet exercice sur l'effet Doppler, nous étudions ce qui se passe lorsque qu'une voiture s'approche d'un piéton. La voiture se déplace le long de l'axe OX à une vitesse constante V et émet un son de fréquence FE. Le piéton se situe à une distance D de l'axe. Tout d'abord, nous devons déterminer cosθ en fonction de X et D. En utilisant les formules trigonométriques, nous savons que cosθ est le côté adjacent sur l'hypoténuse. Ici, le côté adjacent est X et l'hypoténuse est √(D² + X²). Donc, nous avons cosθ = X/ √(D² + X²). Ensuite, nous pouvons utiliser cette formule pour calculer la fréquence reçue (FR) en fonction de X. La formule est FR = FE * (1 + (V * cosθ) / (V du son) * √(D² + X²). Cette transformation de cosθ en X est utile car X est le seul paramètre dont nous disposons. Ensuite, nous examinons quatre graphiques et devons déterminer lequel représente l'évolution de la fréquence en fonction de X. Pour cela, nous pouvons utiliser l'élimination. Nous savons que FR est une fonction décroissante, car plus X augmente, plus la fréquence diminue. De plus, lorsque X = 0, FR doit être égal à FE, car le piéton est directement en face de la voiture. Parmi les graphiques proposés, seul celui de la figure 1 satisfait ces critères. Ensuite, nous analysons comment la courbe évolue si V ou D augmentent. Si V augmente, FR augmente également car V est dans le numérateur de la formule. De même, si FE augmente, FR augmente aussi car FE est un facteur de la formule. En revanche, si D augmente, FR diminue car D est situé dans le dénominateur de la formule. En résumé, lorsque la voiture s'approche du piéton, la fréquence reçue diminue. La figure 1 représente l'évolution de la fréquence en fonction de la distance X. Si la vitesse de la voiture ou la distance entre la voiture et le piéton augmentent, la fréquence reçue augmente. N'hésitez pas à poser vos questions en commentaire.

Casque à réduction de bruit

Dans ce cours, Layla de CEDEO explique le concept de réduction de bruit active sur les casques audio. Lorsqu'on active la réduction de bruit sur nos casques, un signal anti-bruit est émis pour combiner avec le bruit ambiant, ce qui crée l'impression d'absence de bruit. Le cours présente plusieurs configurations de casques : sans casque, avec une réduction de bruit passive (casque isolant) et avec une réduction de bruit active. Un graphique montre comment ces différentes configurations affectent le niveau d'intensité sonore en fonction de la fréquence. Il est expliqué que le casque passif n'est efficace que pour certaines fréquences graves, tandis que la réduction de bruit active est plus efficace dans une zone spécifique (zone B). Dans une autre zone de transition, les deux types de réduction de bruit sont efficaces, mais avec des degrés d'efficacité variables en fonction de la fréquence. Dans la dernière zone, les deux types de réduction de bruit sont également efficaces. 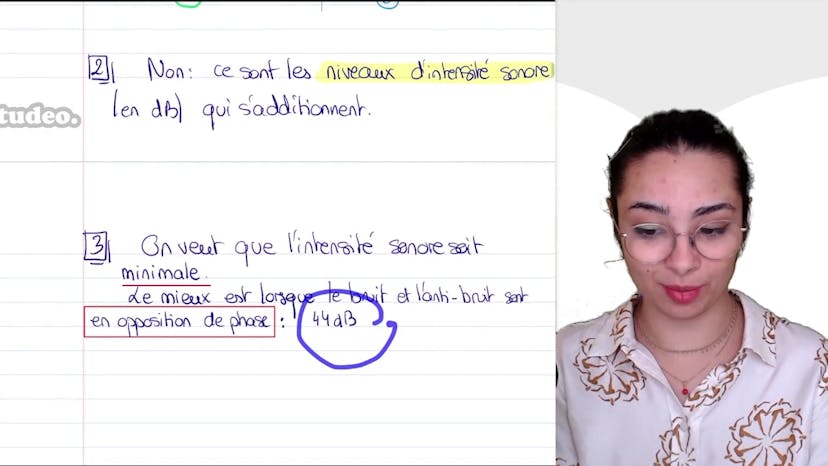Ensuite, le cours aborde la question de l'émission simultanée de bruit et d'anti-bruit dans différentes situations. On explique que ce sont les niveaux d'intensité sonore qui s'additionnent, pas les intensités sonores elles-mêmes. Les niveaux d'intensité sonore sont mesurés en décibels. Enfin, on demande quelle situation est la plus efficace pour le dispositif de réduction active de bruit. La réponse est lorsque le bruit et l'anti-bruit sont en opposition de phase, ce qui entraîne la plus grande atténuation du niveau sonore.

Vélocimétrie Doppler

La vélocimétrie Doppler est une méthode non-invasive pour mesurer la vitesse du sang, souvent utilisée en médecine pour détecter des problèmes vasculaires. On utilise une sonde émettant des ultrasons à une certaine fréquence, les globules rouges affectent ensuite cette onde avec une fréquence différente à cause de l'effet Doppler. On peut déterminer la vitesse des globules rouges en analysant un spectre et en isolant les fréquences correspondant à la fréquence émise et reçue. On applique ensuite une formule pour trouver la vitesse des ultrasons qui nous donne une vitesse d'environ 42 cm par seconde, correspondant à l'ordre de grandeur de la vitesse du sang dans le corps humain.

Musiciens dans un train

Dans cette vidéo, Christophe Buballot a mené une expérience pour vérifier l'effet Doppler en plaçant des musiciens dans un train qui jouaient une note (La 440) et en faisant écouter cette note à des auditeurs le long de la voie. Les auditeurs ont perçu une fréquence différente de la note émise en raison du mouvement de l'onde sonore par rapport à eux. La fréquence reçue dépendait de la note jouée par les musiciens, qui était exprimée en Hertz. En utilisant la formule de l'effet Doppler, la vitesse du train a été calculée à partir de l'écart entre la fréquence émise et la fréquence reçue des notes. La vitesse calculée était de 63,4 km/h, ce qui est raisonnable pour un train de l'époque.

Flux de photons

Dans cette vidéo, Layla explique comment déterminer la force équivalente aux flux de photons reçus par une personne qui est de dos face au soleil. Elle fait le lien entre l'optique géométrique et la physique quantique pour comprendre les interprétations de la lumière. Layla commence par expliquer ce qu'est un flux de photons, qui est le nombre de photons arrivant par mètre carré et par seconde. Elle utilise ensuite les relations de Planck-Einstein pour passer de la puissance à l'énergie, en utilisant la longueur d'onde de la lumière. Layla définit le flux d'une grandeur comme cette grandeur divisée par unité de surface et par unité de temps. Elle donne également la formule pour calculer le flux de photons en utilisant le flux de puissance donné. Ensuite, elle explique comment calculer la quantité de mouvement absorbée par un individu de dos au soleil en multipliant le flux de photons par la surface et le temps. Elle utilise ensuite la deuxième relation de Planck-Einstein pour calculer la quantité de mouvement pour un photon et la multiplie par le nombre de photons reçus. Enfin, elle utilise le principe fondamental de la dynamique pour calculer la force équivalente, en utilisant la variation de la quantité de mouvement par rapport au temps. Layla fait remarquer que les forces issues des photons sont très faibles et peuvent être négligeables à l'échelle humaine, mais peuvent avoir un effet important dans certains domaines, comme la biologie.

Hauteur d'un miroir

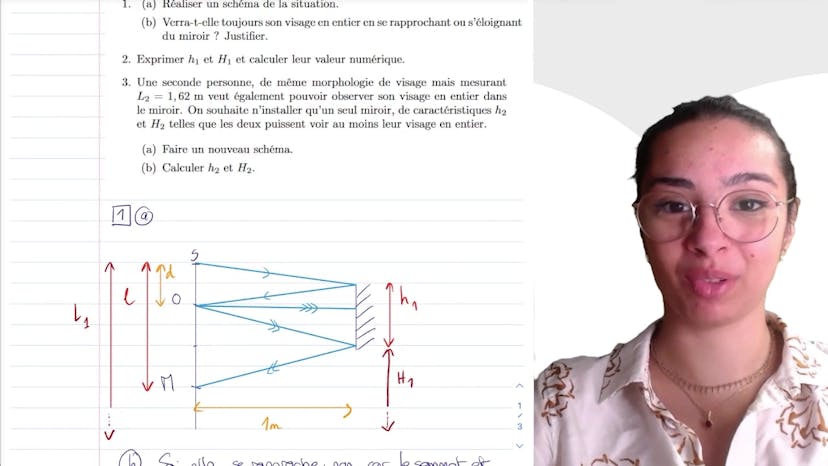
Aujourd'hui, nous allons faire un exercice sur les miroirs. L'objectif est de trouver le miroir qui convient à une personne en fonction de ses critères. La personne mesure 1m85 et la longueur de son visage est de 25 cm. Elle souhaite installer un miroir qui lui permette de voir son visage en entier lorsqu'elle est à 1m de distance. Pour déterminer cela, nous devons tracer un schéma de la situation. En utilisant la loi de Descartes pour la réflexion, nous constatons que le dernier rayon qui provient du sommet du crâne doit se réfléchir à l'extrémité supérieure du miroir, tout comme le rayon provenant du menton doit se réfléchir à l'extrémité inférieure du miroir. Ensuite, nous devons exprimer les hauteurs du miroir. En utilisant la géométrie, nous trouvons que la hauteur du miroir (h1) est égale à la moitié de la longueur du visage, soit 12,5 cm. De plus, la hauteur du miroir par rapport au sol (H1) est égale à la longueur totale du visage moins la hauteur h1, soit 1,67 m. Dans une seconde partie de l'exercice, une deuxième personne plus petite souhaite également observer son visage dans le même miroir. La hauteur du miroir reste inchangée pour la partie supérieure, car la personne la plus grande doit pouvoir voir le haut de son crâne. Cependant, il faut rajouter de la longueur en bas du miroir pour que la personne plus petite puisse voir le bas de son visage. Ainsi, nous trouvons que la hauteur du miroir pour la deuxième personne (H2) est égale à la longueur totale moins la moitié de la longueur plus la distance entre les deux personnes, soit 1,45 m. La hauteur du miroir reste la même pour la partie supérieure. Cet exercice permet de comprendre les principes de la réflexion dans le cadre des miroirs. N'hésitez pas à poser vos questions si vous en avez.

Détecteur de pluie

Aujourd'hui, nous allons parler du détecteur de pluie pour pare-brise. Ce détecteur est un petit instrument qui déclenche les essuie-glaces lorsqu'il détecte de la pluie sur le pare-brise. Pour modéliser le pare-brise, nous utilisons des lames de verre parallèles d'une certaine épaisseur et d'un indice de réfraction de 1,5. Un faisceau de lumière émis par un émetteur arrive au point E à l'intérieur du verre et se réfléchit sur le dioptre. Dans cette question, on nous demande de montrer que tout le flux lumineux revient intégralement au détecteur situé en D. Pour cela, nous devons vérifier s'il y a réflexion totale. En utilisant la formule de la loi de Descartes, nous trouvons que l'angle limite est de 4,8 degrés. Comme l'angle d'incidence est de 60 degrés, qui est plus grand que l'angle limite, il y a bien réflexion totale. Ensuite, on nous demande de déterminer la distance ED. En utilisant la loi de réflexion, nous trouvons que la distance est de 1,7 cm. Lorsqu'il pleut, une fine couche d'eau d'indice 1,33 et d'épaisseur 1 mm se forme entre le verre et l'air. Dans cette situation, le rayon lumineux subit une réfraction en entrant dans l'eau, puis une réflexion en arrivant sur le dioptre avec l'air, avant de repartir dans la même direction. La distance du détecteur est décalée de 0,9 cm. Lorsque le détecteur ne capte plus le rayon, cela signifie qu'il y a une couche de pluie qui dévie le rayon lumineux. Cela indique qu'il faut allumer les essuie-glaces car il pleut. J'espère que cet exercice vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Fibre optique

La leçon porte sur la fibre optique et explique comment les rayons lumineux se déplacent à l'intérieur de celle-ci. Il est expliqué que pour que les rayons lumineux soient guidés à l'intérieur de la fibre, il faut qu'il y ait une réflexion totale sur la surface entre le cœur et la gaine de la fibre. Pour cela, il faut que sin θ soit égal à N1/N2. Ensuite, il est expliqué comment passer de l'angle d'incidence (I) à cet angle limite (θ) en utilisant la loi de Descartes. L'ouverture numérique de la fibre est également définie comme étant N0*sin(IA). Ensuite, on calcule la différence de temps de propagation entre le rayon qui va tout droit et celui qui réfléchit à chaque interface, en utilisant la géométrie. Enfin, on détermine la fréquence minimale des impulsions lumineuses pour qu'elles soient distinctes et on compare la bande passante de la fibre avec celle d'un téléphone portable et de la télévision.

Un mirage

Dans ce cours, Layla nous parle d'un mirage optique. Elle explique que l'air chaud provoque un gradient d'indice optique qui change en fonction de la hauteur. Elle utilise la loi de Gladstone-Dale pour étudier l'évolution de l'indice optique en fonction de la température. Elle nous demande ensuite de ranger les indices optiques par valeur croissante, en se basant sur le fait que l'air le plus proche du sol est le plus chaud. Ensuite, elle explique que les rayons se courbent progressivement à chaque réfraction dans un milieu plus réfringent. Ces rayons donnent l'impression de venir d'en bas et créent ainsi un mirage. Elle introduit ensuite le concept de couches d'air infinitésimales pour modéliser la variation continue de l'indice optique en fonction de la température. Elle explique comment exprimer l'indice optique et les fonctions trigonométriques en fonction de petits variations d'angles et de longueurs. Elle montre ensuite comment on peut exprimer dz/dx en fonction de n0, k et a à l'aide de la loi de Descartes et de formules trigonométriques. Finalement, elle résout l'équation différentielle dz/dx en intégrant et obtient l'équation de la trajectoire du rayon, qui est une parabole. Elle explique que c'est cette trajectoire qui crée l'illusion d'un palmier ou d'une flaque d'eau lorsque les rayons arrivent à l'œil de l'observateur. Layla conclut en rappelant que les mirages optiques peuvent se produire lorsque l'air est chaud et donne des exemples de mirages courants, tels que les flaques d'eau sur le bord de la route. Elle encourage les étudiants à faire l'exercice pour se familiariser davantage avec le sujet et à poser des questions en commentaire.

Refractomètre d'Abbe

Dans cette vidéo, Layla de Studio explique le fonctionnement du réfractomètre d'Abbe, qui permet de mesurer l'indice optique d'un milieu, généralement un liquide ou un gaz. Le réfractomètre d'Abbe est composé de deux prismes identiques et d'un film de liquide dont on cherche à déterminer l'indice optique. Dans la première partie de la vidéo, Layla donne quelques indications sur la résolution de l'exercice. Elle souligne l'importance d'un schéma clair et bien dessiné ainsi que de l'argument physique utilisant le principe de retour inverse de la lumière, qui est souvent applicable dans ce genre de situation. Ensuite, Layla aborde la question de la direction du rayon sortant par la face CD. Elle explique que grâce au principe du retour inverse de la lumière et à la symétrie des prismes, le rayon sortira par la même direction que celle d'entrée. Ensuite, elle explique comment l'angle d'incidence pour lequel un rayon transmute et sort par la face AD permet de déduire la valeur de l'indice du liquide. Elle rappelle que cela est possible uniquement si l'indice du prisme (N0) est supérieur à celui du liquide (N). Layla montre ensuite comment calculer cet angle d'incidence critique à partir de l'angle limite de réflexion totale. Elle indique que cet angle limite peut être déterminé en utilisant la loi de Descartes. Ainsi, en mesurant l'angle à partir duquel le rayon ne sort plus par la face CD mais par la face AD, on peut remonter à l'indice du liquide. Ensuite, Layla donne un exemple chiffré pour illustrer le calcul de l'indice du liquide. Si l'angle d'incidence critique vaut 18°, l'indice du liquide sera de 1,32. Enfin, Layla aborde les limites d'utilisation du réfractomètre d'Abbe. Elle souligne que les principales limitations sont d'ordre géométrique, car il faut mettre un liquide entre deux prismes, ce qui peut compliquer la mesure avec des gaz. De plus, le dispositif fonctionne uniquement lorsque l'indice du prisme est supérieur à celui du liquide, limitant ainsi les mesures à des liquides dont l'indice est inférieur à 1,7 (indice du prisme utilisé ici). Layla recommande donc l'utilisation de ce type de réfractomètre en chimie, pour vérifier des lois d'échelle expérimentales. Elle encourage également les spectateurs à poser leurs questions ou à faire leurs remarques dans les commentaires.