Cours d'apprentissage en ligne

Suivi expérimental

Dans cette vidéo, nous examinons les méthodes pour suivre une réaction cinétique entre le diiode (I2) et le dihydrogène (H2). L'équation de réaction est : H2 + I2 → 2H+ + 2I-. Pour suivre l'évolution de cette transformation, nous utilisons des capteurs adaptés. Si la réaction implique des espèces colorées, nous utilisons un spectrophotomètre pour mesurer l'absorbance de la couleur jaune due au diiode. L'absorbance diminuera au fur et à mesure que le diiode est consommé. Si la réaction implique des espèces chargées, nous utilisons un conductimètre pour mesurer la conductivité. La conductivité augmentera car les espèces chargées sont produites pendant la réaction. Si la réaction implique des ions H+, nous utilisons un pHmètre pour mesurer le pH. Le pH diminuera car des ions H+ sont produits. Il est important de retenir ces méthodes et de savoir les utiliser dans les exercices. En analysant les différentes espèces présentes dans une réaction, nous pouvons choisir la méthode de suivi adaptée. Merci d'avoir suivi cette vidéo et à bientôt !

Etude de graphe

Aucun résumé n'est disponible pour cette vidéo

Rôles annexes

Dans cette vidéo, nous étudions l'influence de certains paramètres de réaction sur la cinétique de celle-ci. Nous avons deux expériences, A et B, avec des mélanges initiaux identiques. L'expérience A est réalisée à 20 degrés tandis que l'expérience B est réalisée à 35 degrés. Nous mesurons la quantité de produits formés pendant des durées égales ΔTj. La première question porte sur le rôle de la concentration des réactifs sur la rapidité d'évolution du système. Il est important de noter que nous ne pouvons pas simplement comparer les expériences A et B car les mélanges initiaux sont identiques. La différence se situe donc dans les différents états du système au fil du temps. Pour un même intervalle de temps, nous formons plus de produits lors de ΔT1 que lors de ΔT2 et ΔT3. Ainsi, nous pouvons conclure que plus la concentration en réactif est élevée, plus la vitesse de réaction est importante. Ensuite, nous examinons le rôle de la température sur la cinétique de la réaction. Nous comparons l'expérience A à 20 degrés avec l'expérience B à 35 degrés. La quantité de produits formés pour chaque intervalle de temps est plus importante à 35 degrés. Nous pouvons donc conclure que plus la température est élevée, plus la vitesse de réaction est importante, conformément à la loi de Van't Hoff. En résumé, nous avons étudié l'influence de la concentration des réactifs et de la température sur la cinétique d'une réaction chimique. Ces questions sont essentielles en synthèse industrielle et dans le domaine de la recherche. Merci d'avoir suivi cette vidéo et à bientôt !

Hydrolyse du saccharose

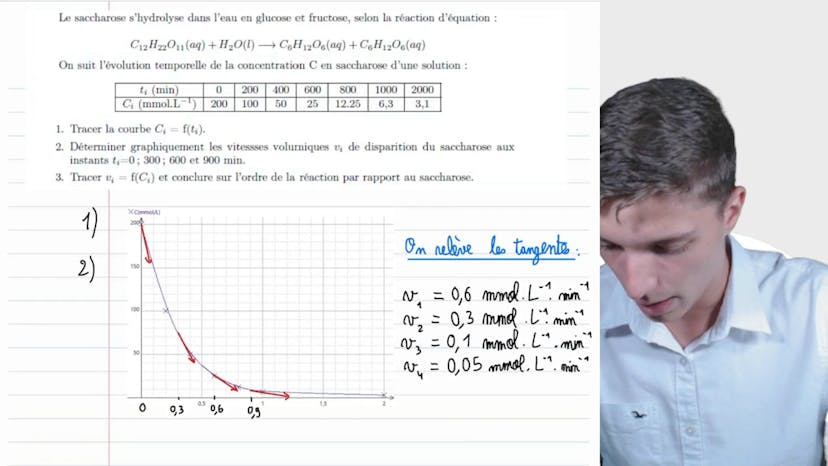
Dans cette vidéo, nous étudions l'hydrolyse du saccharose. Le saccharose se décompose en glucose et en fructose dans l'eau. La réaction est la suivante : C12H22O11 + H2O donne C6H12O6 + C6H12O6. Le glucose et le fructose sont des isomères, ce qui signifie qu'ils ont la même formule brute. Nous observons l'évolution temporelle de la concentration en saccharose dans une solution. La concentration est exprimée en millimoles par litre et le temps en minutes. Il est important de bien repérer les unités pour éviter les erreurs dans les résultats. La première question consiste à tracer la courbe de concentration en fonction du temps. Pour cela, nous utilisons un tableau et le logiciel de régression si disponible. Ensuite, nous déterminons graphiquement les vitesses volumiques de disparition du saccharose aux instants 0, 300, 600 et 900 minutes. La vitesse volumique de disparition correspond à la pente de la tangente à la courbe de concentration en fonction du temps. Elle est positive car il s'agit d'une vitesse de disparition. Les vitesses volumiques de disparition obtenues sont les suivantes : V1 = 0,6 mmol/L/min, V2 = 0,3 mmol/L/min, V3 = 0,1 mmol/L/min, et V4 = 0,05 mmol/L/min. Ensuite, nous traçons les différentes vitesses en fonction de la concentration. Mis à part la dernière mesure qui fausse légèrement les résultats, nous obtenons une droite caractéristique d'une cinétique d'ordre 1. Cela signifie que la vitesse est proportionnelle à la concentration, conformément à l'équation V = k * c. Cette conclusion est également cohérente avec le temps de demi-vie de la réaction, qui est indépendant de la concentration initiale en réactif. Dans une réaction d'ordre 1, le temps de demi-réaction est égal à ln(2)/k et ne dépend pas de la concentration initiale. En conclusion, l'ordre de la réaction par rapport au saccharose est de 1. Il est recommandé de revoir la méthode si vous n'avez pas encore assimilé cette configuration classique de détermination de l'ordre de réaction. Merci d'avoir suivi cette vidéo. À bientôt !

Détermination d'ordres

Bonjour à tous ! Dans cette vidéo, nous allons déterminer les ordres partiels de réaction. Nous étudierons la réaction entre les ions iodure (I-) et les ions fer 3 (Fe3+), représentée par l'équation 2I- + 2Fe3+ -> I2 + 2Fe2+. La vitesse initiale de disparition des ions iodure (VdispI-0) peut être exprimée comme VdispI-0 = K * [I-]initial^alpha * [Fe3+]initial^beta. Nous devons trouver les valeurs des ordres partiels alpha et beta. Nous réalisons deux séries de mesures expérimentales pour déterminer les vitesses initiales de disparition des ions iodure. Dans chaque série, nous fixons la concentration initiale d'une espèce : dans la première série, la concentration d'I- est toujours de 4 mol/l, et dans la deuxième série, la concentration de Fe3+ est de 1,7 mol/l. Dans la première série de mesures, la concentration initiale de I-^0 à la puissance alpha est une constante, que nous pouvons regrouper avec la constante de vitesse K. Ainsi, la vitesse de disparition dépend uniquement de la concentration de Fe3+. Nous pouvons donc tracer VdispI- en fonction de [Fe3+], ce qui nous donne une cinétique d'ordre 1. Dans la deuxième série de mesures, nous traçons Vdisp en fonction de I-^0I à la puissance alpha. Cette relation ressemble à une parabole, typique d'une cinétique d'ordre 2. En considérant que la concentration de Fe3+ est fixée, nous concluons que alpha est égal à 2. Ainsi, nous obtenons la loi de vitesse suivante : la vitesse de disparition des ions I- initial est égale à k * [I-]initial^2 * [Fe3+]initial^1. Cet exercice est essentiel et nous permet de réviser l'analyse classique de la cinétique chimique. Il montre également comment réduire l'ordre global d'une réaction en fixant la concentration d'un réactif. Cette méthode est importante à retenir. Merci de votre attention et à bientôt !

Vocabulaire

Aucun résumé n'est disponible pour cette vidéo

Le lait tourne

Dans cette vidéo sur la chimie cinétique pratique, nous étudions la dégradation du lactose en acide lactique dans le lait sous l'action de bactéries. Cette dégradation, ou "tournage" du lait, se manifeste par un changement de couleur et d'odeur. À une température de 28°C, le lait tourne en 4 heures. Nous voulons savoir combien de temps il faudra pour que le lait tourne au réfrigérateur, où la température est de 5°C. Pour cela, nous disposons des données suivantes : l'énergie d'activation de la réaction est de 75,1 kJ/mol, la concentration de lactose dans le lait suit une loi exponentielle, et la température doit être convertie de degrés Celsius à Kelvin. Nous devons définir la concentration de lactose à partir de laquelle nous considérons que le lait a tourné, notée CL. Selon la loi exponentielle, CL = C0 * exp(-KT), où K est une constante proportionnelle à exp(-Ea/RT), C0 est la concentration initiale de lactose et T est la température du système en Kelvin. Nous pouvons exprimer CL dans le cas de la température chaude (28°C) et dans le cas de la température froide (5°C). En isolant Tlf, le temps limite à partir duquel le lait a tourné à la température froide, nous obtenons l'équation Tlf = Tlc * exp(Ea/RT) * (1/Tf - 1/Tc). En effectuant les calculs appropriés à partir des données fournies, nous trouvons que Tlf est égal à 54 heures, ce qui est beaucoup plus long que les 4 heures à température ambiante. Ainsi, la conclusion de l'exercice est qu'il est préférable de conserver le lait au réfrigérateur pour prolonger sa durée de conservation. En résumé, cet exercice de chimie cinétique pratique aborde la dégradation du lactose dans le lait et démontre l'importance de le conserver au réfrigérateur.

Identification

Dans cette vidéo, on nous présente un étudiant qui a mélangé ses résultats et perdu les valeurs des constantes de vitesse associées à ses courbes de réaction. Les courbes de vitesse d'avancement en fonction de la concentration sont des droites, ce qui caractérise une cinétique d'ordre 1. Pour déterminer chaque constante de vitesse, il faut identifier pour quelle température cela a été fait. La vitesse de disparition à la température T1 est k1 fois c, à la température T2 est k2 fois c, et à la température T3 est k3 fois c. En comparant les vitesses de réaction, on identifie que la température T3 est la plus rapide, suivie de la température T2, puis de la température T1. Ainsi, les coefficients directeurs correspondants sont k1 = 10 secondes^-1, k2 = 43 secondes^-1, et k3 = 63 secondes^-1.

Longueur d'onde

Aucun résumé n'est disponible pour cette vidéo

Angle de diffraction

Cette vidéo explique comment déterminer les angles de diffraction d'une onde sonore lorsqu'elle rencontre une ouverture de largeur donnée. Pour cela, il faut utiliser la relation classique θ en radian, qui est égal à λ en mètres divisé par A en mètres. En utilisant cette relation, on peut trouver l'angle de diffraction en radian, qui peut être converti en degré en utilisant une simple règle de 3 : θ en degré = θ en radian x 180 / π. En se souvenant que les degrés sont une unité plus forte que les radians, on peut facilement se rappeler comment convertir les unités dans les deux sens.

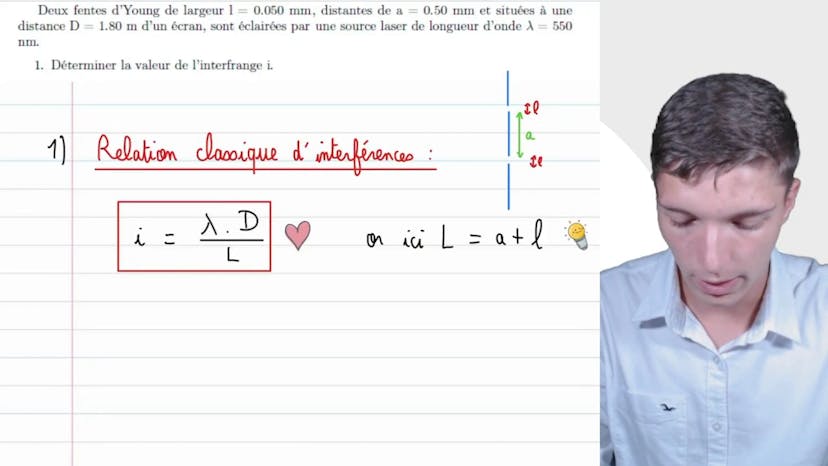
Interfrange

Dans cette vidéo, Matisse de Studio explique comment déterminer la valeur d'une interfrange en utilisant la formule classique des interférences. Il prend l'exemple de deux Fandug de largeur L, éclairées par une source laser de longueur d'onde lambda de 550 nm, à une distance de 1,80 m d'un écran. Il faut alors faire attention car A, la distance entre les franges, inclut la largeur L des fentes. La formule pour l'interfrange I est I = lambda * d / (A+L), où d est la distance entre les fentes et l'écran, et L est la distance entre les deux centres des fentes. Il est important de retenir cette relation pour tous les exercices en interférence. L'application numérique donne une valeur de 1,8 mm pour I.