Cours d'apprentissage en ligne

Un entier toujours impair ?

Dans ce cours, on nous demande de démontrer que pour tout n, la quantité 3n4 plus 5n1 est impaire. On appelle cette quantité "an" pour la suite de la question. Ensuite, on doit en déduire que ce nombre n'est jamais divisible par nn1. Pour cela, on utilise le fait que nn1 est un produit de deux nombres consécutifs et qu'au moins l'un d'eux est pair. On remarque également que nn1 est la somme des entiers jusqu'à n. On utilise ces propriétés pour démontrer que nn1 ne divise pas an. On conclut en montrant que an est paire et an plus 1 est impaire, et que an plus 1 est toujours divisible par 6, tandis que nn1 est divisible par 2. On utilise des décompositions en facteurs premiers pour arriver à ces conclusions.

Piège à éviter : degré 2 !

Dans cette vidéo, nous abordons un exercice mathématique qui peut sembler difficile et effrayant. Il s'agit de déterminer les solutions d'une équation polynomiale avec des congruences. Tout d'abord, il est conseillé de réécrire l'équation en utilisant des lettres plus conventionnelles pour faciliter la compréhension. Ensuite, nous devons appliquer les méthodes classiques pour résoudre le problème en utilisant une table des congruences. Nous pouvons également essayer de factoriser l'équation pour trouver une solution évidente. Si cela ne fonctionne pas, nous continuons avec la table des congruences en testant différentes valeurs pour x. Après avoir rempli la table, nous constatons que les valeurs de x² plus x ne sont jamais congruentes à 3 modulo 5. Par conséquent, l'ensemble des solutions est vide. Il est important de comprendre la démarche de résolution plutôt que de se concentrer sur les concepts mathématiques complexes. En utilisant une approche méthodique et réfléchie, nous pouvons surmonter les difficultés et résoudre ce type de problème. En conclusion, bien que cet exercice puisse sembler intimidant, il est essentiel d'avoir confiance en sa capacité de réflexion et de prendre le temps d'analyser les différentes possibilités. J'espère que ce résumé vous a été utile et je vous invite à me rejoindre dans ma prochaine vidéo.

5²ⁿ, 2²ⁿ ... et des congruences !

Dans cet exercice de congruence, on nous demande de déterminer quand l'expression 2 puissance 2n + 2 puissance n + 1 est divisible par 7. Pour simplifier, nous remplaçons 2 puissance 2n par 4 puissance n et nous cherchons à comprendre le comportement de 4 puissance n et de 2 puissance n. Nous constatons que 4 puissance n suit un cycle : 4 puissance 1 est congruent à 4, 4 puissance 2 est congruent à 2, et 4 puissance 3 est congruent à 1. Donc, nous avons 4 puissance 3k qui est congruent à 1, 4 puissance 3k + 1 qui est congruent à 4, et 4 puissance 3k + 2 qui est congruent à 2. Quant à 2 puissance n, nous remarquons qu'elle suit également un cycle de taille 3 : 2 puissance 3 est congruent à 1, 2 puissance 3k + 1 est congruent à 2, et 2 puissance 3k + 2 est congruent à 4. En combinant ces résultats, nous concluons que pour tout entier n qui est égal à 3k, 3k + 1 ou 3k + 2, l'expression 2 puissance 2n + 2 puissance n + 1 est congruente à 3 modulo 7. En résumé, l'expression est divisible par 7 pour tous les entiers n qui ne sont pas multiples de 3 (c'est-à-dire les pairs et les entiers qui laissent un reste de 1 ou 2 lorsqu'ils sont divisés par 3).

Problème : Suite et PGCD !

Ce cours présente un problème d'arithmétique basé sur une fraction, ce qui est inhabituel car on préfère travailler avec des nombres entiers. Cependant, il est rapidement démontré que A n est un entier. A n est défini comme une suite, ce qui est intéressant car cela permet d'utiliser une formule explicite pour calculer A2 et A3. Ensuite, on nous demande de démontrer une relation de récurrence pour A n+1, ce qui est surprenant car on s'attendait à une formule explicite. En utilisant cette relation et quelques calculs, il est démontré que A n appartient à l'ensemble des nombres entiers. Par la suite, on nous demande de montrer que le PGCD de A n et A n+1 est égal à 1 ou à 3. En utilisant la relation de récurrence précédente, il est prouvé que ce PGCD est égal à 1 ou à 3. Enfin, on nous demande de vérifier que A0 est congru à 1 modulo 3, ce qui est facilement démontré en calculant A0. À partir de là, il est conclu que pour tout n, les A n ne sont pas divisibles par 3. En résumé, ce cours présente un problème d'arithmétique complexe mais avec des techniques efficaces, ce qui permet de résoudre les différentes questions de manière rapide et précise.

Désintégration

Dans cette vidéo, Leïla explique le concept de radioactivité et de désintégration du plomb. Elle présente différents types de radioactivité: alpha, bêta moins, bêta plus et gamma. Elle donne également les nombres de charges et de masses pour les éléments qui se désintègrent, ainsi que les produits de cette désintégration (oxygène, uranium, télénium). Le but est de trouver les équations radioactives qui conservent à la fois le nombre de masses et le nombre de charges. Leïla explique ensuite que les combinaisons possibles sont limitées et nécessitent de trouver des produits qui ont des nombres de charges similaires. Elle conclut en écrivant les équations pour la désintégration du plomb, du plutonium et de l'azote. Elle utilise un positron pour le plomb, une particule alpha pour le plutonium et un électron pour l'azote. Elle encourage les spectateurs à poser des questions dans les commentaires.

Phosphore

Dans cette vidéo, nous abordons le sujet du phosphore et de sa radioactivité. Le phosphore 32 est un isotope radioactif qui se désintègre en un noyau de soufre 32. Notre première tâche consiste à établir l'équation de la désintégration radioactive du phosphore 32 et à identifier le type de radioactivité impliqué. En ce qui concerne les charges atomiques, le phosphore possède 15 protons et le soufre en a 16. Les masses atomiques du phosphore 32 et du soufre 32 sont respectivement de 32 unités. Dans les réactions nucléaires, il existe trois types de sous-produits : les positrons, les électrons et les noyaux d'hélium (particules alpha). Les photons gamma ne sont pas des particules alpha, car ils n'ont ni masse ni charge. Dans notre cas, pour garantir la conservation totale du nombre de charges, il est nécessaire d'introduire un électron. Cette réaction est donc du type de radioactivité bêta, représenté par les symboles plus (+) et moins (-) bêta. J'espère que cette vidéo vous a été utile et n'hésitez pas à poser des questions.

Lois de conservation

Aujourd'hui, nous allons aborder les lois de conservation dans une réaction nucléaire. Il y a deux lois principales à retenir : la loi de conservation des charges électriques (Z) et la loi de conservation des masses (A). La charge électrique correspond au nombre de charges présentes dans le noyau. Lors d'une réaction nucléaire, il est important de conserver cette charge et aucun électron ne doit être perdu. De même, le nombre de masses (protons, électrons et neutrons) doit également être conservé. Nous pouvons également appeler ces lois la loi de Sodie. Lors de la résolution d'exercices de désintégration radioactive, il est essentiel de veiller à la conservation du nombre de masses et du nombre de charges. Ensuite, nous devons compléter les équations de désintégration radioactive en déterminant les valeurs de A (nombre de masses) et Z (nombre de charges). Dans chaque équation, nous devons vérifier que le nombre de masses et le nombre de charges sont conservés. Par exemple, si nous prenons le cas du plomb 182 se désintégrant en tellurium, nous constatons que le nombre de masses reste conservé à 189 et le nombre de charges également conservé à 82. Nous pouvons également observer différents types de radioactivité (alpha, bêta+, bêta-) en fonction des émissions de particules spécifiques dans chaque équation. En résumé, lors d'une réaction nucléaire, il est essentiel de respecter les lois de conservation des charges électriques et des masses. En comprenant et en appliquant ces lois, vous serez en mesure de résoudre correctement les exercices de réactions nucléaires. N'hésitez pas à poser vos questions ou à faire des remarques dans les commentaires.

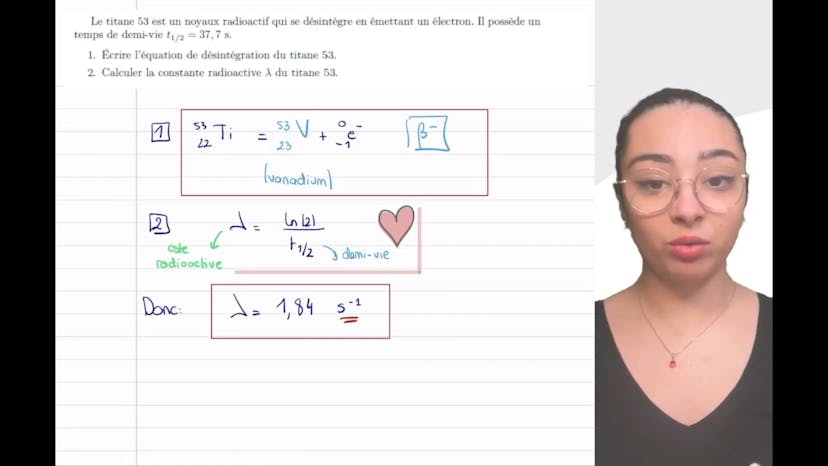
Titane

Aujourd'hui, nous allons parler du titane 53, un rayon radioactif qui se désintègre en émettant un électron. L'équation de désintégration est la suivante : titane 53 se désintègre en émettant un électron, ce qui donne du vanadium. Pour calculer la constante radioactive, nous utilisons la formule lambda = ln(2) / T1/2, où T1/2 est le temps de demi-vie du titane 53. En utilisant cette formule, nous obtenons une valeur de 1,84 avec l'unité en secondes^-1. Assurez-vous de bien utiliser les unités afin d'éviter des erreurs dans vos calculs. N'hésitez pas à poser vos questions en commentaire.

Activité radioactive

Aujourd'hui, je vais vous résumer un cours sur l'activité radioactive de manière SEO-friendly. Dans ce cours, nous étudions un échantillon de roche contenant du cobalt, bombardé artificiellement par des neutrons. L'objectif est de déterminer l'activité radioactive de cette roche. Pour cela, nous utilisons la formule de l'activité radioactive, A = λN, où A représente l'activité en becquerels (Bq), λ est la constante radioactive en secondes inverse, et N est le nombre de noyaux radioactifs à un certain instant. Nous disposons de deux instants différents pour lesquels nous connaissons le nombre de noyaux radioactifs. En utilisant la loi de décroissance radioactive, qui est une fonction exponentielle, nous pouvons lier ces deux valeurs. En isolant la constante radioactive λ, nous obtenons l'expression λ = 1/Tln(N₀/N), où T représente l'intervalle de temps entre les deux instants T₀ et T₁, N₀ est le nombre initial de noyaux radioactifs, et N est le nombre de noyaux restants à l'instant T₁. Ensuite, nous pouvons calculer l'activité radioactive à l'instant T₁ en multipliant λ par N₁, soit A(T₁) = λN₁. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions ou à laisser vos commentaires.

Décroissance radioactive

Aujourd'hui, nous avons analysé une courbe de décroissance radioactive d'un échantillon. Dans cet exercice, nous avons d'abord cherché à déterminer la durée au bout de laquelle 70% des noyaux radioactifs sont désintégrés. En utilisant la loi de décroissance radioactive, nous avons calculé que cette durée était d'environ 10 jours. Ensuite, nous avons estimé la durée au bout de laquelle il n'y aurait plus de noyaux radioactifs dans l'échantillon. Contrairement à une exponentielle continue, une exponentielle discrète, comme celle-ci, peut atteindre la valeur zéro. Nous avons donc cherché à déterminer à quel instant le dernier noyau se désintégrerait. En utilisant la formule ln(n₀/λ), où n₀ est le nombre initial de noyaux et λ est le paramètre de décroissance radioactive, nous avons calculé que cet instant correspondait à 80 jours. Enfin, nous avons exprimé cette durée en termes de demi-vie. Comme nous connaissions la demi-vie de l'échantillon (8 jours), nous avons converti les 80 jours en 10 demi-vies. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Uranium 238

Aujourd'hui, nous allons parler de l'uranium-238 et de son processus de désintégration. L'uranium-238 est un noyau radioactif qui se transforme en plomb-206, un noyau stable, par le biais de plusieurs étapes de désintégration. Ces désintégrations successives mènent à un noyau stable, conformément à la vallée de la stabilité dont nous avons parlé précédemment. La première étape de désintégration conduit à la formation de thorium-234. Il s'agit d'une désintégration radioactive de type alpha, comme le montre l'équation de réaction. Ensuite, le thorium-234 va à son tour se désintégrer, cette fois par une réaction de type bêta-, conduisant à la formation de protactinium-234. L'équation globale de toutes ces désintégrations successives nous permet de déterminer le nombre total de désintégrations radioactives nécessaires pour arriver au plomb-206, qui est considéré comme stable. En analysant l'équation, nous observons qu'il y a un nombre donné d'électrons et de désintégrations, ce qui indique que seules les réactions de type alpha et bêta- ont lieu. En comptant le nombre d'électrons et de particules alpha produits, nous pouvons déduire qu'il y a eu huit désintégrations alpha et six désintégrations bêta-. En additionnant ces deux chiffres, nous obtenons un total de 14 désintégrations avant d'atteindre le plomb-206, qui est stable. J'espère que ce cours vous a été utile. N'hésitez pas à poser vos questions en commentaire.