 All subjects
All subjects
 All subjects
All subjects
Corrigés de BAC
Bac Physique-Chimie
Terminale

Le lancer de gerbe de paille (2)
Le cours aborde le sujet du microphone utilisé lors de la compétition du lancé de gerbe de paille. Le microphone est un transducteur électro-acoustique qui convertit un signal acoustique en un signal électrique. Il est relié à une enceinte acoustique par l'intermédiaire d'un amplificateur de puissance. Le condensateur présent dans le microphone est constitué de deux armatures : une membrane mobile en plastique recouverte d'une fine pellicule métallique et une plaque métallique fixe. Lorsque le microphone ne capte pas de son, la distance entre les deux armatures est de l'ordre de 15 à 25 micromètres. Pour fonctionner, le condensateur doit être chargé avec une source de tension continue. On étudie la phase de charge du condensateur. On établit la relation entre la tension de la source de tension idéale (E), la tension aux bornes du condensateur (UC) et la tension aux bornes de la résistance (UR) en utilisant la loi des mailles. Ensuite, on montre que l'équation différentielle vérifiée par la tension aux bornes du condensateur lors de la charge est de la forme E = RC * (d(UC)/dt) + UC. On mesure la tension aux bornes du condensateur lors de sa charge et on obtient une courbe qui peut être modélisée par trois fonctions mathématiques. On argumente que la troisième fonction correspond à la modélisation de la charge du condensateur en se basant sur les limites des fonctions. On vérifie que la fonction retenue est solution de l'équation différentielle établie précédemment. Ensuite, on utilise la relation entre la capacité d'un condensateur plan et les armatures pour déterminer la valeur de la distance entre les deux armatures du microphone lorsque celui-ci ne capte pas de son. Enfin, on explique que lorsque la distance entre les armatures diminue, la capacité du condensateur diminue également.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Le lancer de gerbe de paille (3)
Dans cet exercice, nous nous intéressons à l'intensité sonore émise par une enceinte et son impact sur la santé.
Une source S est considérée isotrope si elle émet la même quantité d'énergie dans toutes les directions. L'intensité sonore mesurée à une distance d de la source est donnée par la relation I = P / (4πd²), avec I en watts par mètre carré, P en watts et d en mètres.
Le niveau d'intensité sonore L est lié à l'intensité sonore I par la relation L = 10 log(I / I0), où L est exprimé en décibels, I en watts par mètre carré et I0 en watts par mètre carré.
Pour calculer le niveau d'intensité sonore L1 correspondant à une intensité sonore mesurée à une distance d1 de l'enceinte (I1 = 3,2 x 10^-3 watts par mètre carré), on utilise la relation L = 10 log(I / I0) et on trouve L1 = 95 décibels.
La législation européenne fixe des durées limites d'exposition journénière à ne pas dépasser à certains niveaux d'intensité sonore. Pour une intensité de 95 décibels, la limite est de 15 minutes par jour à une distance d'un mètre de l'enceinte.
La puissance P de l'enceinte est calculée en utilisant la relation P = 4πd1²I1, ce qui donne P = 4 x 10^-2 watts.
Les organisateurs d'une manifestation sportive ont fixé à 2 x 10^-4 watts par mètre carré la valeur maximale de l'intensité sonore perçue par le spectateur, correspondant à un niveau d'intensité sonore maximum de 86 décibels. Cette valeur est choisie pour éviter des traumatismes.
Pour vérifier si la distance de sécurité de 3 mètres entre les barrières et l'enceinte est suffisante pour respecter la valeur maximale d'intensité sonore, on calcule la distance maximale à respecter en utilisant la relation d = √(4πImax), avec Imax = I0 x 10^(Lmax / 10). On trouve une distance maximale de 1,8 mètres, donc une distance de 3 mètres est suffisante.
En conclusion, grâce aux différentes mesures prises, les spectateurs ne subissent pas de séquelles trop graves malgré une exposition de deux heures à une intensité sonore élevée.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Acide benzoïque (1)
Dans cette vidéo, Théobald de Cydéo se penche sur un exercice de chimie du BAC de 2022 en Nouvelle-Calédonie portant sur la réaction de l'acide benzoïque avec l'eau.
L'exercice propose de calculer la masse nécessaire pour préparer une solution d'acide benzoïque, en utilisant la concentration donnée (C0) et le volume de la solution (V0). En utilisant la formule de la concentration molaire, Théobald explique comment calculer la quantité de matière (N0) correspondant à cette masse et comment remonter à la masse (M0) grâce à la masse molaire.
Ensuite, l'exercice demande de déterminer si la solution est saturée en se référant à la solubilité de l'acide benzoïque. Théobald explique que si la concentration de l'acide dans la solution est égale à la solubilité maximale (2,4 g par litre), alors la solution est saturée. En effectuant le calcul, il conclut que la solution n'est pas saturée.
L'exercice suivant consiste à écrire l'équation de réaction de l'acide benzoïque avec l'eau. Théobald explique que l'acide réagit avec l'eau pour former l'ion benzoate et l'acide H3O+. Il vérifie ensuite que l'équation est équilibrée en s'assurant que tous les réactifs sont présents à gauche et tous les produits à droite.
Ensuite, l'exercice demande de tracer le diagramme de prédominance du couple acide benzoïque/ion benzoate et de préciser l'espèce prédominante dans la solution. Théobald suggère de tracer un axe de pH en indiquant le pKa donné dans l'énoncé. Il explique que la concentration de base est égale à la concentration d'acide au pKa. En se référant à la valeur de pH de la solution (3,1), il conclut que l'acide benzoïque est prédominant dans la solution.
Ensuite, l'exercice demande de compléter un tableau d'avancement en fonction des différentes quantités (C0, V0, X, Y). Théobald rappelle qu'il faut utiliser les quantités en quantité de matière et non en masse. Il remplit le tableau en indiquant les réactifs initiaux, les produits formés et les quantités correspondantes.
L'exercice suivant demande de calculer l'avancement maximal de la réaction en prenant en compte le réactif limitant (l'acide benzoïque). Théobald explique que si tous les réactifs ont été consommés, l'avancement maximal correspond à la quantité initiale de l'ion benzoate (Xmax). Il effectue le calcul et obtient la valeur de Xmax (1,0 fois 10 moins 3 mol).
Enfin, l'exercice demande de montrer que le taux d'avancement final s'écrit sous la forme de la concentration en H3O+ à l'équivalence divisée par C0. Théobald explique que le taux d'avancement final correspond à l'avancement réel divisé par l'avancement maximal. Il effectue les calculs et obtient la valeur du taux d'avancement final (7,9 fois 10 moins 2) qui confirme que l'acide benzoïque est prédominant dans la solution.
Théobald conclut la vidéo en annonçant qu'il poursuivra l'exercice dans une autre vidéo et invite les spectateurs à poser des questions s'ils en ont.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Acide benzoïque (1)
Dans cette vidéo, Théobald de Cydéo explique comment corriger un exercice de chimie du BAC de l'année précédente sur la synthèse de l'acide benzoïque. Il recommande de lire rapidement l'exercice, en soulignant les étapes clés de la synthèse. Les facteurs cinétiques qui permettent d'accélérer la réaction sont la température élevée, la concentration élevée et la présence d'un catalyseur. On utilise un montage à reflux pour chauffer la réaction sans perdre de matière. Pour calculer la quantité de matière d'alcool benzoïque dans un échantillon de 2 mL, on utilise la masse molaire et la masse volumique de l'alcool benzoïque. Dans la deuxième partie de l'exercice, on doit calculer la quantité de matière théorique d'acide benzoïque obtenue en supposant que la transformation est totale et que l'alcool benzoïque est le réactif limitant. En utilisant les stoichiométries des réactions, on peut déterminer que la quantité de matière d'acide benzoïque est égale à la quantité de matière d'alcool benzoïque introduite initialement. Le rendement de la synthèse est calculé en comparant la masse théorique maximale avec la masse réelle obtenue. Le rendement de la synthèse est de 61%. Il est important de noter que le rendement dépend de la nature de la réaction et de son degré de complétion.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Qualité des eaux souterraines (1)
Bonjour à tous, dans cet exercice de chimie des solutions, nous traitons de la contamination de l'eau douce sur les littorales. L'eau de mer salée peut pénétrer dans les nappes phréatiques et contaminer l'eau douce. Selon la concentration en ions chlorure, l'eau peut être potable (inférieure à 150 mg/L), potentiellement contaminée (entre 50 et 200 mg/L) ou impropre à la consommation (au-dessus de 200 mg/L). La concentration minimale en masse d'ions chlorure pour considérer une intrusion est de 200 mg/L.
Dans la deuxième question, nous devons déterminer la concentration en quantité de matière des ions chlorure apportés par le chlorure de magnésium (MgCl2). Nous considérons uniquement la dissolution de MgCl2. En utilisant un tableau d'avancement, nous arrivons à une concentration en ions chlorure de 8,0 x 10^-2 mol/L.
Dans la troisième partie, nous devons calculer la concentration totale en masse des ions chlorure dans la mer Méditerranée. Nous avons la concentration massique (Cm) en ions chlorure apportée par le chlorure de sodium (NaCl) qui est de 16,5 g/L. En utilisant la concentration molaire (C) et la masse molaire des ions chlorure, nous pouvons calculer la concentration massique apportée par la dissolution de MgCl2, qui est de 2,8 g/L. En additionnant les deux concentrations massiques, nous obtenons une concentration totale en masse des ions chlorure dans la mer Méditerranée de 19,3 g/L.
La suite de cet exercice sera abordée dans la prochaine vidéo. N'hésitez pas à poser vos questions en commentaire.
Corrigés de BAC
Bac Physique-Chimie
Terminale
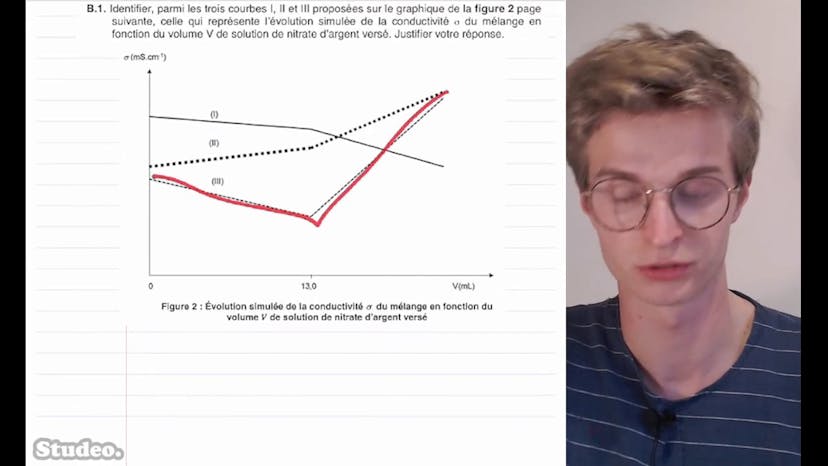
Qualité des eaux souterraines (2)
Dans cette vidéo, on aborde le titrage des ions chlorures dans les eaux souterraines. On explique que la contamination des eaux phréatiques peut se produire si l'eau douce est proche de la mer et si elle contient une concentration élevée d'ions chlorures. On réalise donc un titrage pour mesurer la concentration en masse des ions. On prélève 50 millilitres d'eau douce que l'on titrera avec une solution de nitrate d'argent. On suit le titrage par conductimétrie et on nous demande d'identifier la courbe qui représente la réalité parmi trois différentes. On fait un schéma pour visualiser le dispositif expérimental et on dresse un tableau des ions présents en solution. On comprend que jusqu'à l'équivalence, les ions Ag+ ne sont pas présents en solution et que la concentration en ions Cl- diminue alors que la concentration en ions Ag+ augmente. La conductivité diminue également. À l'équivalence, il ne reste plus d'ions Cl- en solution, mais on continue d'ajouter des ions Ag+. Après l'équivalence, les concentrations en ions Ag+ et NO3- augmentent. On trace ensuite la courbe de conductivité en fonction du volume versé. La courbe qui descend et remonte est la bonne courbe. On nous dit que le volume à l'équivalence est de 13 mL et on veut déterminer si l'eau peut être utilisée pour l'alimentation en eau potable. On utilise la formule de la concentration massique en ions chlorures et on obtient une concentration de 92,13 mg/L, ce qui est inférieur à la limite de 200 mg/L pour l'eau potable. Donc l'eau douce peut être utilisée pour l'alimentation en eau potable. Ensuite, on réalise une modélisation du titrage en utilisant le langage de programmation Python. On veut visualiser l'évolution des quantités de matière des ions Ag+, Cl- et du produit ionique AgCl au cours du titrage. On identifie les espèces A, B et C et on complète une ligne du programme Python pour calculer la concentration en quantité de matière en ions chlorures.
Corrigés de BAC
Bac Physique-Chimie
Terminale
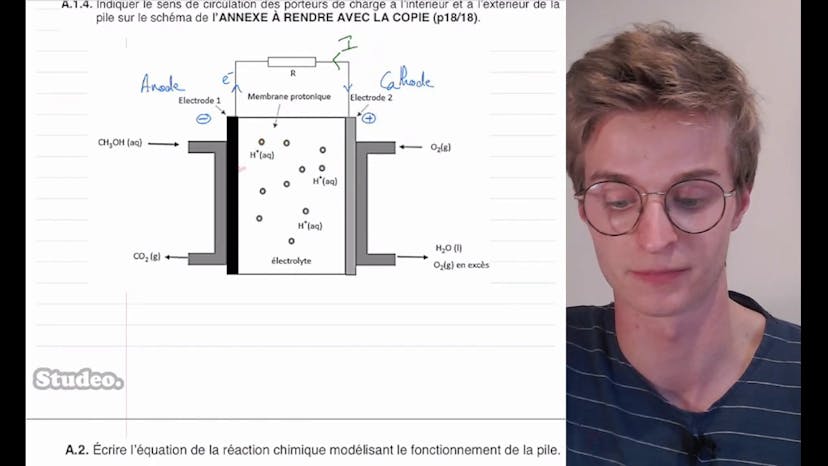
Pile à méthanol (1)
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Physique-Chimie
Terminale

Pile à méthanol (2)
Dans cette vidéo, Obaldesudéo aborde un problème ouvert sur la pile au méthanol qui a été donné au bac l'année dernière. Dans la première partie de l'exercice, Obaldesudéo explique le fonctionnement de la pile au méthanol. Ensuite, il aborde le cas où des élèves veulent faire fonctionner un petit ventilateur avec cette pile au méthanol en utilisant deux piles en série. L'intensité du courant mesurée est de 450 mA et le rendement de chaque pile est de 70%. Toutes ces informations seront utiles pour la partie B de l'exercice.
La première question de cette partie demande de calculer la capacité électrique théorique de la pile au méthanol étudiée dans la partie A. Pour cela, Obaldesudéo rappelle que la capacité électrique théorique est le nombre de moles échangées lors de la réaction, multiplié par la constante de Faraday (9,65 x 10,4 coulombs par mole). Dans le cas de la réaction avec le méthanol, il y a 6 moles d'électrons échangés par mole de méthanol. Donc la capacité électrique théorique est égale à 6 fois la quantité de matière en méthanol introduite dans la pile, multipliée par la constante de Faraday. En faisant le calcul, on obtient une capacité électrique théorique de 16,9 x 10^3 coulombs.
Ensuite, Obaldesudéo aborde la question ouverte où les élèves souhaitent faire fonctionner leur ventilateur pendant au moins une heure. Pour répondre à cette question, Obaldesudéo explique qu'il faut prendre en compte la capacité électrique réelle de la pile. Pour passer de la capacité électrique réelle à la capacité électrique théorique, il faut utiliser le rendement de la pile qui est de 70%. Donc la capacité électrique réelle est égale au rendement fois la capacité électrique théorique. Sachant qu'il y a deux piles en série, la capacité électrique réelle est donc deux fois la capacité électrique réelle de la pile A.
À partir de la capacité électrique réelle, on peut calculer le temps de fonctionnement de la pile en utilisant la formule : capacité électrique réelle = courant multiplié par le temps de fonctionnement. En connaissant la capacité électrique réelle, le courant et en utilisant les chiffres significatifs, on peut trouver le temps de fonctionnement de la pile en secondes.
En utilisant ces informations, Obaldesudéo donne la réponse à la question ouverte. En faisant les calculs, on obtient un temps de fonctionnement de la pile de 5,9 heures. Donc les élèves pourront faire fonctionner leur ventilateur pendant largement plus d'une heure.
Obaldesudéo conclut la vidéo en invitant les spectateurs à poser des questions en commentaire et en donnant rendez-vous pour une prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Indigo et carmin d’indigo (1)
Dans cette vidéo, Matisse de Studio corrige un sujet d'anal sur la spécialité de physique de l'épreuve du Baccalauréat Général de 2022 en Amérique du Nord. Il explique comment lire les entêtes du sujet et vérifier les informations importantes telles que la durée de l'épreuve (3h30) et le matériel autorisé (calculatrice avec mode examen activé et mémoire de type collège). Il souligne également l'importance de s'assurer que le sujet est complet avant de commencer.
Matisse explique ensuite que les candidats doivent traiter 3 exercices, dont l'exercice 1 obligatoire et 2 autres choisis parmi les 3 proposés. Il conseille de se baser sur ses points forts et points faibles pour choisir les exercices les plus adaptés. Il rappelle également les pages où rendre les documents-réponses.
Ensuite, Matisse détaille l'exercice 1, qui concerne la synthèse de l'Indigo. Il explique les différentes étapes du protocole de synthèse et rappelle les données importantes telles que les masses molaires et les masses volumiques de l'acétone. Il aborde les questions de l'exercice, notamment l'identification des groupes caractéristiques et des familles fonctionnelles sur la formule topologique de l'Indigo, le calcul des quantités de matière introduites de 2-nitrobenzaldéhyde et d'acétone, et l'identification du réactif limitant pour déduire la masse maximale d'Indigo pouvant être obtenue.
Enfin, il explique comment calculer le rendement de la synthèse chimique en utilisant la masse finale obtenue et la masse maximale théorique d'Indigo, et conclut en indiquant que le rendement obtenu est de 78%, ce qui est un ordre de grandeur habituel.
Dans la partie B de la vidéo, Matisse continuera à corriger le sujet en abordant d'autres aspects liés à la teinture d'un tissu avec l'Indigo.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Indigo et carmin d’indigo (2)
La partie 1C de ce cours concerne la réaction chimique de l'indigo avec l'oxydant. Lorsque le tissu imprégné de la forme réduite de l'indigo (Inde H2) est exposé à l'air, l'oxydation de l'Inde H2 se produit, ce qui conduit à la formation de l'indigo. L'oxydant responsable de cette transformation est le dioxygène (O2) présent dans l'air. L'indigo oxydé reste piégé dans le tissu et lui donne ainsi sa couleur bleue. L'exposition à l'air est donc essentielle pour que l'indigo se forme et donne la teinte caractéristique au tissu.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Indigo et carmin d’indigo (3)
Dans cette vidéo, Mathis de Studio nous parle du carmin d'indigo, un indicateur coloré acido-basique. Il nous explique que le carmin d'indigo est utilisé pour déterminer la valeur de la constante d'acidité du couple acide-base correspondant. Il commence par nous donner des informations générales sur le carmin d'indigo, comme le fait qu'il soit un colorant bleu de synthèse E132 et qu'il imite l'indigo.
Ensuite, Mathis nous présente les données disponibles pour résoudre l'exercice. Il nous parle des couples acide-base impliqués dans la réaction, H2O, HO-, H3O+, et H2O. Il nous explique que l'équation de la réaction est HIN + H2O = IN- + H3O+ et qu'il est possible de calculer le taux d'avancement final de la réaction en utilisant un tableau d'avancement. Il montre également comment relier le taux d'avancement final au caractère total ou non total de la transformation.
Ensuite, Mathis nous demande de montrer que l'expression de la constante d'acidité Ka du carmin d'indigo peut s'écrire en fonction du pH de la solution à l'équilibre et de sa concentration en quantité de matière initiale. Il explique comment exprimer la constante d'acidité Ka en utilisant les concentrations à l'équilibre des différentes espèces et comment les relier aux concentrations initiales.
Ensuite, Mathis nous demande de déterminer la valeur de la constante d'acidité Ka du couple acide-base et d'en déduire la valeur de son pKa. Il effectue les calculs nécessaires et obtient une valeur de Ka de 2,5 10^-12 et un pKa de 11,6.
Enfin, Mathis discute de l'utilisation de cet indicateur coloré pour le titrage d'un acide chlorhydrique par une solution d'hydroxyde de sodium. Il montre que la zone de virage de l'indicateur se situe autour de pH 11,6 et que le pH à l'équivalence du titrage est de 7, ce qui est bien en dehors de la zone de virage de l'indicateur. Il conclut donc que le carmin d'indigo n'est pas adapté pour ce titrage car il ne change pas de couleur à l'équivalence.
En résumé, cette vidéo traite de la partie C de l'exercice 1, qui concerne le carmin d'indigo en tant qu'indicateur coloré acido-basique. Mathis explique les concepts liés à cet indicateur, résout les calculs nécessaires pour déterminer la constante d'acidité Ka et le pKa, et discute de son utilisation dans un titrage.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Indigo et carmin d’indigo (4)
Dans cette vidéo, Mathis de Studio aborde la dernière partie de l'exercice 1 d'une annale portant sur l'utilisation médicale du carmine d'indigo. Le carmine d'indigo est utilisé pour colorer l'urine en bleu afin de réaliser certains diagnostics médicaux. L'objectif de cette partie est de déterminer la concentration en masse de la solution injectable de carmine d'indigo, afin de calculer le volume maximal à injecter sans dépasser la dose journalière admissible. Le carmine d'indigo absorbe au maximum dans les 620 nanomètres, ce qui lui donne une couleur bleue. Pour préparer une solution de concentration donnée, il faut utiliser un protocole de dilution en se basant sur les équations classiques de facteur de dilution. En réalisant un étalonnage, on peut déterminer la concentration de la solution nécessaire. En utilisant ces informations, on peut calculer le volume de solution S à injecter en fonction de la dose journalière admissible pour un patient donné. Il est important de prendre en compte les différentes notations et de garder à l'esprit l'objectif de chaque partie de l'exercice. Dans cette vidéo, Mathis aborde également les différents matériels et techniques utilisés pour réaliser les mesures nécessaires.


