Home

2BAC SM Maroc

Maths SM&SP

Analyse

Rappels sur les définitions de limites

Lorsque nous parlons des limites de fonctions avec x tendant vers un réel a, nous avons deux cas principaux. Dans le premier cas, la fonction F tend vers l'infini ou moins l'infini. Dans le deuxième cas, la fonction F converge vers une valeur finie. Nous nous concentrerons d'abord sur ce deuxième cas, qui est plus simple mais aussi un peu bizarre.

L'idée est que lorsque x se rapproche de a, la courbe de la fonction suit son cours normal et nous amène à différents points. Cela correspond à la notion de continuité, que nous étudierons plus en détail ultérieurement. Par exemple, si nous prenons la limite de x + 3 lorsque x tend vers 2, nous obtenons simplement 2 + 3, soit 5.

Cependant, il existe des cas plus complexes, comme la limite de sin(x)/x lorsque x tend vers 0. Il s'agit d'un cas bizarre car cela donne 0/0, ce qui n'est pas évident à évaluer. Pour éviter cette division par 0, nous choisissons de définir la fonction sin(x)/x sur R* (l'ensemble des réels à l'exception de 0). Dans ce cas, il est possible de démontrer que la limite vaut 1.

Sur un graphe, nous pouvons voir que la fonction sin(x)/x encadre le point (0,1) avec deux branches qui se rapprochent de ce point. Cela montre qu'il s'agit bien d'une limite où x tend vers 0 et la fonction converge vers 1.

En ce qui concerne les limites infinies, nous utilisons la notion de plateau qui bloque la fonction. Pour pouvoir dépasser n'importe quel plateau, nous utilisons la définition suivante : F tend vers plus l'infini si F est indépassable par un plateau. Par exemple, pour une hyperbole, nous constatons que peu importe la taille du plateau, la fonction finira par le dépasser. Cela définit la notion de tendeur plus infini.

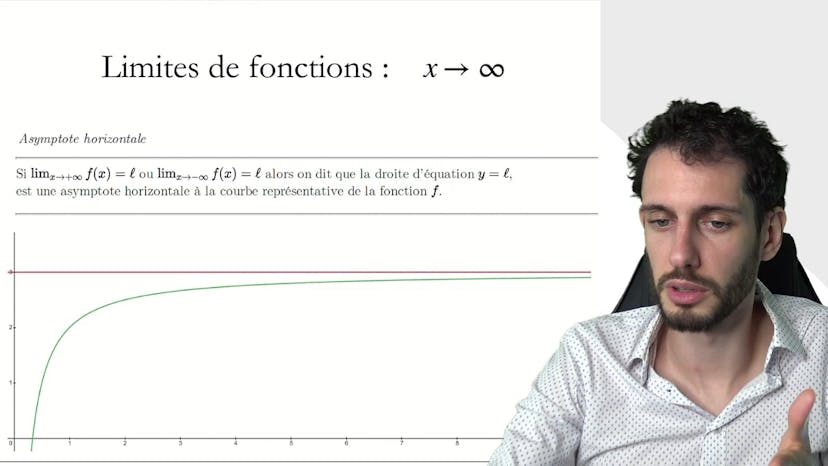
Finalement, nous introduisons la notion d'asymptote verticale, qui est une droite à laquelle la fonction se colle lorsque x tend vers plus ou moins l'infini et a une limite plus l'infini en un point fini. Par exemple, lorsque la limite à gauche ou à droite de f(x) lorsque x tend vers a est infinie, nous appelons la droite x=a une asymptote verticale.

En résumé, nous avons étudié les limites de fonctions lorsque x tend vers a. Dans certains cas, les fonctions tendent vers l'infini ou converge vers une valeur finie. Nous avons également introduit la notion d'asymptote verticale pour les limites plus l'infini en un point fini. N'hésitez pas à poser des questions supplémentaires ou à discuter avec d'autres dans la FAQ.

Quand on parle de limite de fonction avec X qui tend vers un réel A, on va avoir deux cas. Les deux cas principaux, c'est F qui finit par partir vers plus ou moins l'infini, et l'autre cas c'est F qui va converger vers une valeur finie. Je vais commencer par ce cas là, il est plus simple et aussi un peu bizarre. Donc là vous allez me dire, ouais ok, X s'approche de A, F s'approche de L, c'est juste en fait la courbe qui suit son cours normal, et on suit la courbe comme ça, et voilà, on arrive sur des points. Alors ça oui, c'est une notion qu'on verra qui s'appelle la continuité. Donc c'est un chapitre ultérieur. C'est vrai qu'il y a des cas très simples, par exemple, si je vous donne un exemple un peu bêbête, la limite de X plus 3 quand X tend vers 2, vous allez me dire, ah oui ok, t'es gentil, ça fait donc 2 plus 3, ça fait 5. Très simple, et c'est vrai que c'est très simple, mais il faut faire la définition, voilà. Ça va aussi s'appliquer à des cas un peu plus vicieux ou bizarres, du genre, si je prends un truc comme ça. Sinus X sur X, en 0, ça fait, la limite de sinus X en 0, sinus 0, 0, sur 0, ça nous fait du 0 sur 0. 0 sur 0 c'est pas évident. Et donc déjà, sinus X sur X, la fonction, si je la définis comme un objet fonction, je dois dire que son ensemble de définition c'est R étoiles. Je ne peux pas inclure 0, sinon je suis obligé d'écrire sinus 0 sur 0, et j'écris une division par 0, crise cardiaque de tous les problématiques, c'est pas possible. Donc là j'ai un cas bizarre, et en fait, il est faisable, il est possible de démontrer que cette limite vaut 1. Donc on a une limite quand même, qui est finie, pour un X qui s'approche d'un réel. Je vais vous montrer à quoi ça ressemble en gros sur le graphe. Comme vous le savez, j'adore cette fonction sinus X sur X, je l'utilise pour tous mes exemples. Sur ce graphe, si j'ai un petit point qui se balade par exemple, là vous le voyez un peu sur la courbe, l'ogiciel n'est pas capable de me tracer ce point, quand j'ai mis un point en haut pour abscisse X, pour ordonner f2x, f2x étant sinus X sur X, le point n'est pas capable d'afficher la valeur 0, parce qu'il sait que ce point, cet abscisse 0, est interdit pour la fonction sinus X sur X. Encore une fois, on ne peut pas diviser par 0. Et pourtant, quand je zoom, alors là on ne le verra pas sur le graphe, mais c'est un peu l'idée, quand je zoom, en fait l'idée c'est que les deux parties, il y a deux parties pour cette fonction, deux branches si vous voulez, une qui part d'un côté et une qui part de l'autre de la même manière symétrique, viennent se rapprocher de plus en plus du point 1, mais c'est comme si à chaque fois je devais exclure juste le petit point d'abscisse 0 et d'ordonner 1. Donc j'ai un peu deux branches qui viennent encadrer ce point là. Donc là c'est aussi une limite, enfin c'est un cas de limite intéressant, où on a bien le X qui tend vers 0, un réel, et la fonction qui tend vers un nombre réel, 1. Avant de détailler un peu plus la définition de la limite infinie, qui en gros utilise la notion de plateau, comme on a déjà vu pour les suites, ou pour la limite des fonctions, quand les fonctions partent en plus infini, quand X tend lui-même vers plus infini, donc il y a cette notion de, en gros on tend vers plus infini lorsqu'on est toujours capable de dépasser n'importe quel plateau, qui essaye de nous bloquer. J'ai envie de définir la petite définition suivante, qui est un peu la définition de la notion de s'approcher d'un point, en gros limite à gauche, limite à droite. Donc si je veux m'approcher d'un point A, en fait j'ai deux manières de le faire, soit je viens par valeur supérieure, donc je m'approche par ici, hop hop hop hop hop, comme ça et j'arrive par des valeurs au-dessus de A et je diminue, par exemple si A ça vaut 5, je vais vers 7, 6, 5, 5,5, etc. Ou par valeur inférieure, tiens je viens d'ici, je fais hop hop hop, 2, 3, 4, 4,5, et j'approche de A égale 5. Donc je peux m'approcher d'un nombre de deux côtés, par au-dessus, par en dessous. Donc les deux phénomènes, on va appeler ça 1, la limite quand on vient de la gauche, par valeur inférieure, et 2, la limite quand on vient par la droite, par valeur supérieure. Et on va noter ces différents cas de comment atteindre la limite, donc ces différents cas de limite comme ceci, X tend vers A avec X plus petit que A ou X plus grand que A. Donc si je reviens sur la définition en plus infini maintenant, c'est là-dessus, c'est surtout en plus infini qu'on va utiliser ces petites nuances, en fait qu'est-ce que c'est tend vers plus infini ? C'est comme d'habitude donc, on va dire F tend vers plus infini si F est indépassable, si F n'arrive pas à se faire bloquer par un plateau de données. Donc je vais vous montrer un petit peu cette notion. Voilà donc un exemple, j'ai une hyperbole ici, j'ai pris une hyperbole et je me rends compte que, si j'ai un plateau en rouge, c'est mon plateau A, si je prends un plateau de taille quelconque, laissez-moi changer un peu l'échelle ici, voilà, si je prends un plateau de taille quelconque, disons A égale, je ne sais pas, 5 ou 7. Pour un plateau de données, est-ce que c'est vrai qu'à un moment, quand je m'approche de plus en plus de la valeur 5, donc ici je prends la valeur 5, j'ai l'impression que c'est là que ça va commencer à partir un peu en vrille, est-ce qu'en m'approchant de plus en plus de la valeur 5, donc mon X tend vers 5, en l'occurrence ici par la droite, par la gauche, excusez-moi, est-ce que ma fonction va toujours finir par dépasser ce plateau ? Oui. Apparemment, quand j'arrive à 4,85, je dépasse le plateau. Vous pourriez me dire, ok, très bien, mais est-ce que ça marche pour tous les plateaux ? En effet, si je prends un plateau de plus en plus grand, et là j'arrive à 40, 50, je pars très loin, est-ce que ma fonction va toujours finir par dépasser ce plateau ? Si je super-zoom dessus comme ça, je vois que oui. C'est ça la définition de tendeur plus infini. C'est cette même notion d'être indépassable quel que soit le plateau, quand X tendait vers plus l'infini, partait complètement dans l'infini, pardon, dans cette direction. Là, c'est la même chose, X ne fait que s'approcher, s'approcher, s'approcher, et pourtant on monte super vite et on est imbloquable. Là, ça permet de définir notamment cette droite au milieu là. Comme ça, on a l'impression qu'on se colle quand même à une droite verticale. Ça permet, sur le même modèle de l'asymptote horizontal, de définir la notion de droite dans laquelle on se colle, c'est-à-dire asymptote verticale. On va expliquer dans ces cas-là, lorsqu'on a une limite en un point fini qui est égale à plus ou moins l'infini, on va appeler cette droite X égale 5, en l'occurrence, cette droite verticale, une asymptote. C'est la dernière définition d'asymptote du programme, donc on avait l'asymptote horizontal, quand il y a une limite finie en plus ou moins l'infini, asymptote oblique, c'est un petit bonus que je vous ai donné, et ensuite asymptote vertical, quand il y a une limite plus l'infini en un point fini. On peut écrire ça comme ça. Petit bilan, si la limite à gauche ou et à droite de f2x quand x tend vers a est infinie, on appellera la droite X égale a une asymptote verticale. Voilà, ça c'était le petit bilan sur tout ce qu'il y avait à savoir sur les limites de fonction lorsque x tend vers a. N'hésitez pas à me poser des questions, demander plus de détails si besoin, discuter avec les autres dans la FAQ. Je vous retrouve dans la prochaine vidéo.

En un point réel, limite infinie

RELATED

Recommended videos

Introduction Limites

En l'infini, limites finies et infinies

Les asymptotes horizontales