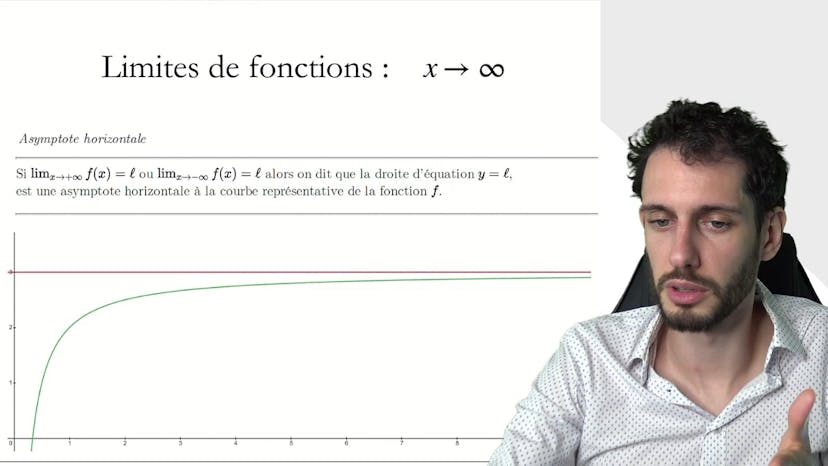
All subjects
All subjects
 All subjects
All subjects
Calcul de limite finie avec la définition (trouver un epsilon)
Dans ce cours, nous étudions le calcul de la limite finie. Nous avons déjà examiné la notion de limite infinie et nous nous concentrons maintenant sur une limite spécifique fixée, utilisant la définition avec les épsilon.
Pour comprendre comment utiliser les épsilon, nous les utilisons pour montrer que la fonction tend vers moins l'infini, de manière similaire. Peu importe la limite fixée, aussi petite soit-elle, il y aura nécessairement un moment où la fonction sera inférieure dans une plage de valeurs négatives. En fait, lorsque je serai à une distance de épsilon proche de 1, je serai en dessous de cette limite. Donc, l'idée est que j'aurai un intervalle du type 1-épsilon1 où la fonction sera inférieure à M. J'ai donné quelques exemples avec la fonction 1/(x-1) pour illustrer cela.
La méthode est la même, nous partons de l'inégalité f(x) ≤ M et nous essayons de résoudre f(x) - M pour trouver l'encadrement de x qui nous permettra de déterminer le épsilon approprié.
Nous commençons avec un réel M négatif et regardons la limite en 1- pour x-1. Nous résolvons f(x) - M, ce qui donne 1/(x-1) - M. Nous examinons ensuite 1/(x-1) - M ≤ 0, et sachant que la fonction inverse est décroissante sur ℝ*, nous devons vérifier si nous sommes sur ℝ- ou ℝ+. Nous souhaitons encadrer x, nous devons donc avoir x > 1-1/M, en tenant compte du fait que 1/M est négatif. Ainsi, nous avons l'encadrement voulu : x < 1 et x > 1-1/M.
Maintenant, nous avons notre épsilon, qui est égal à 1-1/M. Si nous prenons épsilon de cette valeur, dans tout l'intervalle 1-épsilon à 1, notre fonction f(x) sera inférieure à M, ce qui correspond exactement à ce que nous voulions démontrer.
Ainsi, nous avons démontré rigoureusement, en utilisant les calculs de limites, les définitions et les épsilon, que la limite lorsque x tend vers 1- (par valeurs négatives de 1/(x-1)) est égale à moins l'infini.
Il est important de s'exercer avec des exercices équivalents pour mieux comprendre la méthode.
En résumé, pour utiliser cette méthode, nous partons de l'inégalité f(x) ≤ M et nous trouvons l'épsilon approprié en utilisant 1-1/x, en déroulant progressivement.
C'est tout pour cette méthode.