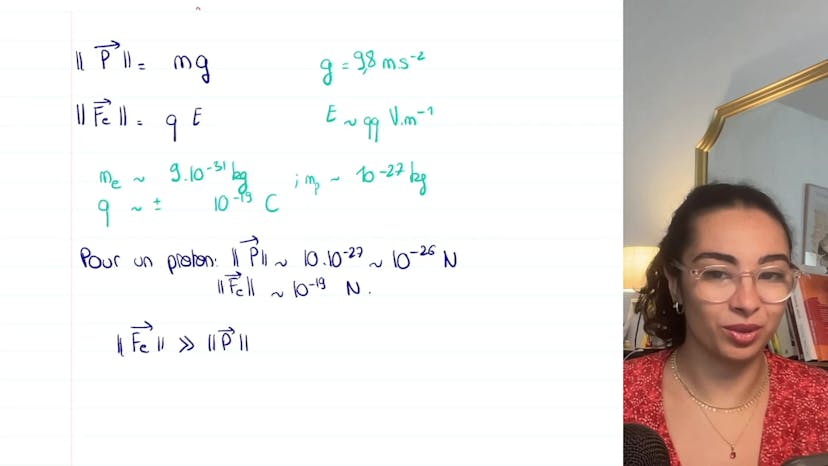Home

MPSI/PCSI

Physique-Chimie

Physique

Mouvement d'une particule chargée

Aujourd'hui, nous allons étudier le mouvement cyclotron, une démonstration classique sur les particules chargées. Nous considérons une particule de charge Q et de masse M qui évolue dans un champ magnétique B selon l'axe OZ. La particule a une vitesse initiale selon l'axe EY. L'objectif est de déterminer le mouvement de la particule dans cette configuration. Nous négligeons le poids de la particule et ne considérons que la force magnétique.

Nous commençons par rappeler les expressions des vecteurs vitesse (V) et accélération (A) en coordonnées cartésiennes et les appliquer au Principe Fondamental de la Dynamique (PFD). Pour calculer la force de Lorentz, nous utilisons la formule QV ⊗ B. En projetant cette force sur les deux directions qui nous intéressent, nous obtenons les équations X = QBY/M et Y = QBX/M, que nous appelons équations couplées.

Nous voulons résoudre ces équations couplées. Une méthode consiste à dériver l'équation pour obtenir une équation de la forme d'un oscillateur harmonique. Une autre méthode consiste à utiliser une grandeur intermédiaire complexe U = X' + Y'. En dérivant U par rapport au temps, nous obtenons une équation de la forme U' = - Y ωc U, où ωc est la pulsation cyclotronique (QBM).

Nous résolvons cette équation en fonction des conditions initiales pour obtenir U(t) = IV0e^(-iωct). Cependant, U n'a pas de sens physique, donc nous séparons sa partie réelle (qui correspond à VX) de sa partie imaginaire (qui correspond à VY). Finalement, nous obtenons X(t) = V0 sin(ωct) et Y(t) = V0 cos(ωct), ce qui représente le mouvement de la particule dans le plan XY.

Nous intégrons encore une fois ces équations pour obtenir les expressions de X(t) et Y(t) en fonction du temps. Ainsi, nous trouvons X(t) = V0/(ωc) (1 - cos(ωct)) et Y(t) = V0/(ωc) sin(ωct). La trajectoire de la particule correspond à ces équations et elle forme un cercle. Nous le démontrons en utilisant le théorème de Pythagore pour éliminer les cos² et sin².

La vitesse de la particule sur le cercle est constante et égale à V0, tandis que sa vitesse angulaire est égale à ωc. Cela signifie que la particule parcourt le cercle à une vitesse constante et avec une vitesse angulaire déterminée par les propriétés du champ magnétique. 

Dans le cas d'une particule de charge négative, les équations restent les mêmes, à l'exception du signe de ωc, qui devient négatif. Cela entraîne des changements dans les coordonnées du centre du cercle, mais la trajectoire reste un cercle.

En conclusion, l'exercice du mou

Bonjour à tous, aujourd'hui on va faire un exercice sur le mouvement cyclotron. Donc j'insiste vraiment, c'est l'exercice le plus important de tout votre chapitre sur les particules chargées. Pourquoi ? Parce que c'est une démonstration super classique qu'on va très souvent vous demander en concours, que ce soit à l'écrit ou à l'oral. Allons-y pour la démo. Donc on vous dit qu'on considère une particule de charge Q et de masse M qui est dans un champ magnétique B qui est selon OZ et elle arrive avec une certaine vitesse initiale qui est selon EY. Tout le but ici ça va être de déterminer le mouvement de la particule dans cette configuration-là. C'est ce qu'on appelle le mouvement cyclotronique. Évidemment on vous dit que le poids de la particule est négligé et qu'on ne considère que la force magnétique. Première chose, on vous demande de rappeler les expressions des vecteurs V et A en coordonnées cartésiennes dans les trois directions et d'appliquer le PFD. C'est plutôt sympa comme question. Normalement les vecteurs en coordonnées cartésiennes vous les connaissez. La vitesse est X.Y.Z. L'accélération c'est X seconde, Y seconde, Z seconde. En cartésienne il n'y a pas de difficulté, il suffit juste de dériver à chaque fois la position. La force de Lorentz c'est QV vectorel B et donc là moi j'aime bien placer les vecteurs en colonne donc j'ai le vecteur V ici et j'ai le vecteur B ici. Pour calculer le produit vectorel je fais la règle du gamma ou je sais pas comment vous l'appelez ou les produits croisés. Par exemple pour calculer la composante en Z je fais ça moins ça. C'est la même chose pour toutes les composantes. Donc ici ça va me faire QY.B moins X.B et 0 selon Z. Je projette sur les deux directions qui m'intéressent, il ne se passe rien selon Z donc j'ai un mouvement qui a deux dimensions et ça me donne X. égale à QBY. sur M, Y. égale à QBX. sur M. Donc là on a des équations qu'on appelle les équations couplées. C'est à dire que j'ai X, j'ai Y mais X dépend de Y et Y dépend de X. Donc quand on a un système d'équations comme ça, ce qu'il faut faire pour trouver les équations de mouvement c'est les découpler. Nous ce qu'on aimerait c'est avoir une équation uniquement sur X ou uniquement sur Y. Et pour ça il y a plusieurs techniques. Donc dans le cas général vous pouvez regarder si dans vos deux équations vous arrivez à faire apparaître une combinaison linéaire des deux par exemple, quelque chose qui va permettre d'annuler un terme ou l'autre. Ici ça ne va pas marcher directement, de faire des sommes, des différences. Quelque chose qui va bien marcher, qu'on ne va pas faire ici mais je vous dis quand même si vous voulez faire l'exercice, c'est de dériver. Là si je dérive, j'ai X dérivé trois fois, donc là de l'autre côté je vais avoir du Y seconde. Donc je vais pouvoir faire intervenir cette équation là et je vais avoir une équation de la forme d'un oscillateur harmonique. C'est une manière de faire, ici c'est pas ce qu'on fait. Vous pouvez vous entraîner à le faire, c'est vraiment pas beaucoup plus compliqué. Je pense par contre que ça demande un peu plus de calcul que la méthode qu'on fait. C'est une autre méthode qui consiste à passer par une grandeur intermédiaire en complexe, qui est la grandeur U, qui est X point plus Y point. C'est la vitesse complexe. Et donc si je dérive U par rapport au temps, ça fait X seconde plus Y seconde, ça rien ne change. Et qu'est-ce qui est intéressant, c'est justement les propriétés intéressantes de Y, c'est que comme Y carré est égale à moins 1, si je prends la première équation plus Y fois la deuxième, j'obtiens X seconde plus Y seconde est égale à oméga C Y prime plus Y X prime. Donc vous voyez que ça, ça fait en fait du moins I U. Et donc j'obtiens une équation sur la forme compacte qui va être U point est égale à moins Y oméga C U. Là je ne vous l'ai pas rappelé mais oméga C c'est le même, c'est l'application importante pour les champs magnétiques, c'est QB sur M. Donc voilà, on a réussi à découpler nos équations parce qu'on a réussi à exprimer une seule équation qu'on peut résoudre. On peut la résoudre pourquoi ? Parce qu'à droite et à gauche, on a la même grandeur qu'est U. En plus c'est une équation du premier ordre, donc ça c'est plutôt simple à résoudre. On vous demande ensuite de résoudre l'expression, de déterminer l'expression de U de T en fonction des conditions initiales. C'est une équation du premier ordre, donc il n'y a pas de questions à se poser, la forme c'est lambda E moins omega CT et U de 0 c'est I V0. Pourquoi ? Parce qu'en 0 vous n'avez pas de vitesse selon X, elle est uniquement selon Y. Donc l'un dans l'autre, ça vous donne que U de T c'est I V0 E moins I omega CT. Vous ici, ça ne vous intéresse pas vraiment cette grandeur U, on l'a vraiment introduite uniquement pour pouvoir résoudre l'équation différentielle. Ce n'est pas une grandeur qui a du sens physiquement. Ce qui a du sens par contre, c'est ce qui se passe selon X et ce qui se passe selon Y. Donc maintenant qu'on a fait ça, on peut exprimer U en fonction de la partie réelle et de la partie imaginaire, on va pouvoir les séparer parce qu'on sait que la partie réelle, ça va vous donner VX et la partie imaginaire, ça va vous donner VY. Donc c'est ce qu'on fait ici et on trouve que X. c'est V0 sin omega CT et Y. c'est V0 cos omega CT. Donc voilà, on a réussi à découpler nos équations, on a réussi à les résoudre. On a l'expression de X. et l'expression de Y. en fonction du temps. Alors maintenant ce n'est pas fini, nous ce qui nous intéresse c'est la trajectoire. Donc on va les intégrer encore une fois pour voir ce qui se passe pour la position. Donc si j'intègre la première ici, ça me fait X de T est égal à moins V0 sur omega C cos omega CT plus une constante, et cette constante elle est égale à 0 puisqu'au départ je suis à la position initiale. Donc finalement ça me donne que X de T c'est V0 sur omega C facteur de 1 moins cos omega CT. Même chose pour Y de T, donc on va avoir V0 sur omega C sinus de omega CT. Et la constante est nulle pour la même raison, parce que Y de 0, je ne l'ai pas précisé, mais c'est égal à 0. Maintenant la trajectoire, parce que là vous voyez on a le mouvement, on a des cosinus, des sinus, donc on se doute que ça va être un mouvement périodique. Et donc là on vous donne l'équation d'un cercle, on vous demande de montrer que la trajectoire dans ce cas là c'est un cercle. Là encore une fois, c'est pour ça que cet exercice il est vraiment très formateur, c'est un grand classique. Et il faut partir de l'équation de la relation fondamentale du cosinus et du sinus, qui est le théorème de Pythagore, qui est sin2 plus cos2 est égal à 1. Donc on va exprimer en fait cos2 et sin2, et on va ensuite les éliminer et remplacer par du X et du Y. Comme ça on va avoir une chance de tomber sur l'équation d'un cercle. Donc allons-y, cos2 de ωct c'est 1 moins ωc sur V0 X le tout au carré, comme on a juste interprété ces deux formules là, et sin2 de ωt c'est pareil, ωc sur V0 fois Y le tout au carré. Et donc l'un dans l'autre, si je remplace juste cette formule là, qu'est-ce que j'ai ? J'ai V0 sur ωc moins X au carré plus Y au carré est égal à V0 sur ωc le tout au carré. Donc c'est l'équation d'un cercle. Le rayon on le retrouve ici, le rayon c'est V0 sur ωc, la position du centre ça va être Xc est égal à V0 sur ωc, Yrc est égal à 0. Donc là on a tout ce qu'il faut, et on peut le dessiner. Donc là vous voyez, vous avez un certain rayon, et on remarque que le rayon en fait c'est aussi Xc. Donc qu'est-ce que ça veut dire ? C'est dire que je vais passer par le point 0. C'est logique évidemment comme c'était la position initiale, mais c'est toujours bien de le retrouver dans les équations. Donc là on passe ici, et donc dans ce cas là, notre cercle est parcouru comme ça. Donc ça c'est ce qui se passe si Q est positif, parce que du coup la pulsation propre va être positive. Vous vous souvenez, on a vu dans un autre exercice qu'est-ce qui se passe sur le sens de parcours d'un cercle de cette trajectoire là, et on a vu que selon le signe de Q ça changeait. On a vu que Q positif c'était le sens indirect et Q négatif c'était le sens direct. On nous demande ensuite de montrer que le cercle est parcouru à vitesse constante et à vitesse angulaire oméga c. Donc la vitesse c'est X point, donc on a X point, on a Y point, la vitesse c'est racine de X point carré plus Y point carré. Encore une fois on peut utiliser la relation fondamentale sur les cosinus et les sinus pour voir que 1 plus sine carré, pardon j'ai dit n'importe quoi, sine carré plus cos carré c égal à 1, et donc on retrouve que cette vitesse en norme c'est V0. Là j'ai noté V comme ça, c'est vrai qu'en fait c'est la norme de la vitesse, c'est plus parlant comme ça. C'est logique, parce que vous vous souvenez on a dit que la force électrique elle donnait de l'énergie aux particules, elle pouvait les accélérer ou les décélérer, mais par contre la force magnétique, la partie magnétique de la force de Lorentz, elle a tendance à faire tourner les particules mais elle ne leur apporte pas d'énergie. Donc si elle ne leur apporte pas d'énergie, elles ne peuvent pas accélérer ou décélérer, donc forcément la vitesse est constante. Maintenant pour la vitesse angulaire, sur le cercle la vitesse angulaire c'est R fois oméga, et donc oméga c'est V0 sur R et c'est oméga c. On retrouve bien la pulsation propre qui est la vitesse angulaire. Maintenant qu'est-ce qui change pour une particule de charge négative ? Donc là on peut regarder directement ce qui se passe dans l'équation du cercle. Vous voyez que là on avait oméga c positif, c'était ça l'impact de Q supérieur à 0, c'est oméga c supérieur à 0. Donc là je peux reprendre directement l'équation du cercle et regarder ce qui se passe si oméga c est négatif. C'est la seule chose qui va changer. Toutes les autres équations ça reste exactement le même parce qu'en fait on n'a jamais utilisé le fait que ce soit positif ou négatif à part quand on a tracé ce schéma ici. Donc si on change dans l'équation du cercle, l'équation du cercle c'était ça et donc vous voyez que là c'est à cet endroit là que ça va changer. Là c'est si j'ai utilisé le fait que oméga c c'est valeur absolue de Qb sur m. Donc là vous voyez j'avais un signe moins, ici je vais avoir un signe plus, c'est la seule chose qui va changer, et oméga c l'est également présent ici, mais là c'est le rayon qu'on met au carré, donc ça change rien. Et donc là Q négatif, je vais être dans le sens direct, et la position du centre en x va changer, je vais avoir un xc négatif. Là j'ai xc qui est égal à moins v0 sur oméga c. Voilà pour ça, j'espère que ça vous aura été utile, gardez bien en tête que c'est l'exercice le plus important. Il y a beaucoup d'étapes, en fait là vous voyez qu'il est super guidé, mais en général on pourrait vous poser la question vraiment comme ça, déterminer l'équation de la trajectoire, tracer la trajectoire, etc. Donc gardez bien en tête tout ce qu'on a fait ici. Principe fondamental de la dynamique, on a abouti à des équations qui étaient couplées, on les a découplées en faisant intervenir une grandeur complexe, on a résolu les équations. Pour la trajectoire, autre astuce, on utilise l'équation fondamentale des cosinus et des sinus, cos² plus sin² est égal à 1, et enfin on trace les différentes trajectoires en se référant à l'équation d'un cercle. Et ensuite, après c'est que des questions sur... après c'est des petits raffinements, mais ça c'est vraiment les grandes lignes super importantes à garder en tête.

Mouvement cyclotron

RELATED

Recommended videos

Poid et force électrique

Électrode

Puissance de la force de Lorentz