Home

MPSI/PCSI

Physique-Chimie

Physique

Inductance propre, inductance mutuelle

Dans cette vidéo, Matisse de Studio explique un montage permettant de mesurer le coefficient d'inductance mutuelle entre deux bobines. Le premier circuit est classique avec une force électromotrice, une résistance et une bobine L1, tandis que le deuxième circuit est simplement une bobine L2. L'objectif est de déterminer l'intensité parcourant la bobine 2 et la tension U2 en fonction de la tension U1 et du coefficient d'inductance mutuelle M.

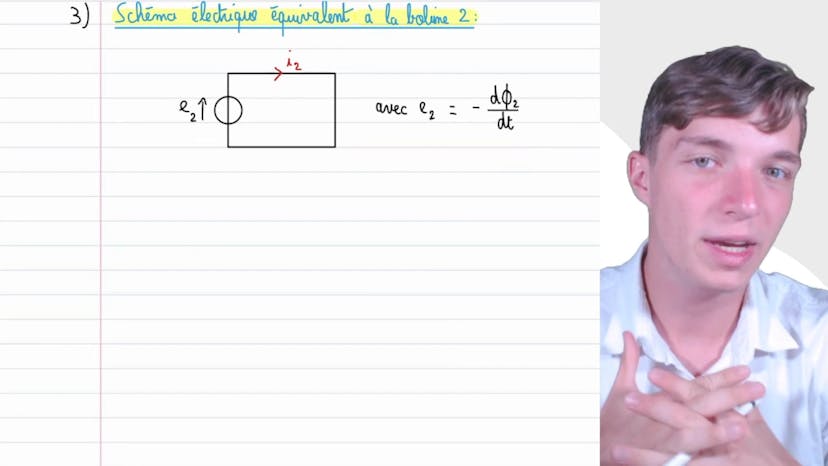
D'abord, il est souligné que la bobine 2 est en court-circuit, donc aucune force électromotrice ou condensateur ne peut délivrer un courant dans ce circuit, ce qui signifie que l'intensité I2 est égale à 0. Ensuite, il est expliqué que la tension U2 dans le cadre de la loi classique de comportement de la bobine est égale à 0, car la tension aux bornes de la bobine 2 serait toujours nulle.

Cependant, étant donné que le circuit 2 est plongé dans le champ magnétique créé par le circuit 1, les bobines sont affectées, ce qui perturbe les courants et les tensions résultants. Il est donc nécessaire de prendre en compte le circuit 1 dans l'expression de la tension U2 en utilisant le concept d'inductance mutuelle.

La troisième question aborde donc l'expression de U2 en fonction de M et U1. L'inductance mutuelle est définie comme le flux du champ magnétique créé par le circuit 1 sur le circuit 2. On introduit également la notion d'auto-inductance, qui est le flux généré par le circuit 1 sur lui-même. Finalement, on obtient l'expression de U2 en fonction de I1, nécessitant de déterminer la relation entre I1 et U1 en utilisant la loi d'Ohm.

Il est alors expliqué que lorsqu'il y a une dérivée dans la relation entre U1 et U2, comme c'est le cas ici, il est utile de passer par les nombres complexes pour simplifier les calculs. En utilisant les grandeurs complexes correspondant au régime sinusoidal forcé, on trouve que le coefficient d'inductance mutuelle M est égal à rU2/(2πfU1).

En appliquant les valeurs numériques données dans l'exercice, U1 = 3V et U2 = 0.5V, on peut calculer M, qui est égal à 1.3 milli Henry.

Ensuite, l'exercice demande de déterminer sans calcul la modification de M lorsque la bobine est tournée à 180 degrés et à 90 degrés. Lorsque la bobine est tournée à 180 degrés, seule l'inversion des branchements de l'oscilloscope se produit, donc M reste sensiblement le même. En revanche, lorsque la bobine est tournée à 90 degrés, très peu de lignes de champ magnétique du circuit 1 traversent la bobine 2, ce qui donne un coefficient d'inductance mutuelle d'environ 0.

En conclusion, cet exercice détaillé permet de comprendre comment mesurer le coefficient d'inductance mutuelle entre deux circuits grâce à un montage particulier.

Bonjour à tous, c'est Matisse de Studio, et dans cette vidéo, on va étudier un montage particulier qui va nous permettre de mesurer le coefficient d'inductance mutuelle M. Alors on étudie ici un montage permettant de mesurer l'inductance mutuelle entre les deux bobines, je ne vous ai pas menti, et bien on a ces deux circuits qui sont couplés juste ici, le premier assez classique avec une force électromotrice, une résistance et une bobine L1, et l'autre simplement une bobine L2. On nous donne les données juste ici, R qui est 100 Ohm, la tension E0 est harmonique, de fréquence f, 2 kHz, et les oscilloscopes mesurant U1 et U2 sont supposés idéaux. Donc c'est un oscilloscope en fait qui mesure la tension aux bandes de la bobine L2, donc il y a un concept. Bien justement, on demande, première question, de déterminer I2, l'intensité parcourant la bobine 2. En fait, la bobine 2 est en court circuit, il n'y a aucune force électromotrice ou condensateur qui pourrait être mis en série dans le circuit 2 qui pourrait délivrer un courant. Le circuit est ici ouvert, donc I2 est égal à 0. Et à ce moment-là, la question qui nous est posée, que vaut la tension IU2 dans le cadre de la loi du comportement habituel de la bobine ? Il faut expliquer pourquoi cette loi ne s'applique pas ici. La loi classique qu'on connaît, qu'on a posée en régime sinusoidal forcé, c'est tout simplement la tension aux bandes de la bobine qui est U2, qui est égale à L2, D2I2 sur DD. Donc forcément, égale à 0, la tension U2 que l'on relèverait serait toujours égale à 0 dans ce cadre-là. Mais ici, il y a quelque chose de particulier, bien sûr, on a placé un autre circuit juste à côté. Et donc, quelle est l'influence de ce circuit ? On l'a déjà un peu touché du doigt. Ici, le circuit 2, en fait, il est plongé dans le champ magnétique créé par le circuit 1. Et ça affecte d'autant plus les bobines, puisqu'elles ont énormément de fils électriques enroulés. Comme nous l'avons vu, ceci perturbe les courants et les tensions résultants. Ainsi, nous devons prendre en compte le circuit 1 dans l'expression de la tension U2. Et donc, on va parler d'inductance mutuelle, bien sûr. Troisième question, donnez justement U2 en fonction de M et de U1. Alors, quelle est cette inductance mutuelle ? Comment est-ce qu'elle se manifeste ? J'ai simplement rappelé la définition de l'inductance mutuelle. Le flux du champ magnétique créé par un circuit 1 sur un circuit 2, il est noté grand-phi de 1 vers 2, qui est égal à M fois I1. Ici, si on parle du flux généré par le circuit 1, c'est donc I1. M, le coefficient d'inductance mutuelle que l'on cherche à déterminer. Et donc, il y a une force électromotrice résultante E qui est égale à moins M dv1 sur dt, dans le cadre d'un schéma électrique de cette façon. Et dans le cas particulier, bien sûr, où l'on étudie l'influence du circuit sur lui-même, on parle d'auto-inductance, et on note phi de 1 vers 1, qui est égal à Li1, avec le coefficient d'auto-inductance. Donc ici, qu'est-ce qu'on a ? D'après ce qu'on a établi, U2, c'est L dvI2 sur dt, avec le flux du champ propre, mais ici, it est égal à 0, puisque I2 est égal à 0, plus ce qu'on a déterminé ici, le flux issu de la mutuelle inductance, M dv1 sur dt, en fonction du temps. Donc ici, on voit ce que l'on obtient, on a U2 en fonction de I1, nous ce qu'on veut, c'est UU2 en fonction de U1, donc il faut déterminer la relation entre I1 et I1, et tout simplement, d'après la loi d'Ohm, vu qu'on regarde la tension au borne d'une résistance traversée par le courant I1, c'est donc I1 qui est égal à U1 divisé par R. Et donc au final, on a U2 de t, qui est égal à M sur R, d2U1 sur dt, en fonction du temps. Voilà ce que l'on obtient. Alors maintenant, on sait d'après l'oscilloscope que U1 est égal à 3V, et U2 est égal à 0,5V, on nous demande de calculer M. Et là, avec nos outils classiques, on est assez embêté, vu qu'il y a une dérivation d'écart entre les deux, U2 est égal à un coefficient fois d2U1 sur dt. Donc si on veut raisonner en termes d'amplitude, ça ne fonctionne pas, lors d'une étude classique. Lorsqu'on est très souvent bloqué dans les exercices d'induction, dans l'exercice d'équations de grandeur couplées entre deux circuits, on va passer par les complexes. S'il y a une dérivation d'écart dans la seule relation dont on dispose, une des solutions, si ce n'est la solution, en tout cas une solution qu'il y a toujours à considérer, c'est de passer par les complexes. Ça nous sauve la vie. Dans le cadre du régime sinusoidal forcé, par cette tension E0, on pose les différentes grandeurs complexes que j'ai détaillées déjà. U2 complexe exponentielle de j oméga t, U1 complexe exponentielle de j oméga t, et on va tout simplement les introduire dans la relation dont on dispose, ce qui va nous simplifier la vie en ce qui concerne les dérivations. Donc ici, on a tout simplement U2 exponentielle de j oméga t qui est égal à m sur r j oméga U1 complexe exponentielle de j oméga t. Très bien, on peut simplifier les exponentielles et prendre les modules. On a tout simplement le module de U2 complexe, c'est m oméga divisé par r fois le module de U1 complexe. Donc finalement, on peut en déterminer le coefficient d'ahutance mutuelle, m c'est égal à r U2 divisé par 2pi f fois U1. On peut passer à l'application numérique, m est égal à 1,3 milli Henry. Donc voilà, c'est la manière dont on l'a déterminée dans cet exercice-là, c'est encore différent des autres, mais très souvent, très très très très très souvent, on va passer par les complexes, puisqu'elles nous sauvent la vie dans ce cadre d'équations couplées. Alors maintenant, on fait tourner la bobine sur elle-même. Dans le plan du schéma, lorsque l'angle de rotation va au 180, déterminer la modification de m sans calcul. Et même question pour un angle de rotation de 90. Donc si on fait tourner ici la bobine sur elle-même, elle va se retrouver tout simplement la tête à l'envers en soi, tout simplement le courant s'écoulera dans le sens inverse. Donc la bobine de 180 degrés reste sensiblement la même, ce sont simplement les branchements de l'oscilloscope qui sont inversés. Donc m à 180 degrés, c'est 1,3 milli Henry. De toute façon, m, il faut le voir comme une grandeur conventionnée, une grandeur que l'on pose par convention, donc son signe n'a pas trop d'intérêt, puisque c'est nous qui posons le signe des courants que l'on étudie. Et dans le cadre de 90 degrés, si on la tourne à 90 degrés, si on reprend le schéma juste ici, si on tourne dans ce sens-là, il y a très peu de lignes de champ du champ magnétique du circuit 1 qui vont traverser la bobine 2. C'est tout ce qui nous intéresse, c'est tout ce qui constitue le phénomène d'induction. Donc avec très peu de lignes de champ qui vont traverser effectivement les vecteurs surface pour chaque spire, on a le coefficient d'inductance mutuelle à 90 degrés qui est environ égal à 0. Voilà, c'est la fin de cet exercice assez complet sur la manière dont on aborde l'inductance mutuelle entre deux circuits. N'hésitez pas à le reprendre de votre côté pour avoir les idées au clair. Merci beaucoup d'avoir suivi cette vidéo, et puis à bientôt.

Mesure de M

RELATED

Recommended videos

Circuits couplés

Bobine longue

Solénoïdes emboîtés