Home

MPSI/PCSI

Physique-Chimie

Physique

Régime sinusoïdal forcé et filtrage

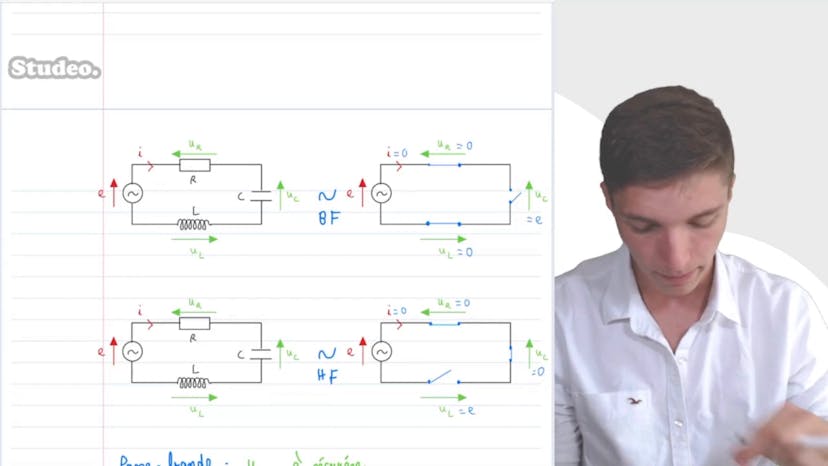
Dans cette vidéo, Matisse de Studio explique comment établir une équation différentielle en utilisant les complexes. L'équation à déterminer est 4 tau² d2u sur dt2 plus 5 tau du sur dt plus U est égal à E. À l'aide d'un diviseur de tension, la tension U peut être exprimée en fonction d'une tension intermédiaire U1, qui peut ensuite être exprimée en fonction de la tension de départ E. En utilisant des manipulations de grandeurs complexes, Matisse détermine l'impédance équivalente et applique le diviseur de tension pour obtenir la relation entre U et E en complexe. En repassant ensuite en réel, l'équation différentielle est obtenue. Cette méthode démontre la puissance de la résolution à l'aide des complexes pour obtenir des résultats électro-signétiques de manière plus simple.

Bonjour à tous, c'est Matisse de Studio et dans cette vidéo on va établir une équation différentielle via les complexes. Alors c'est une vidéo pour vous donner encore plus envie de travailler avec des complexes puisque justement en les utilisant on demande de montrer que la tension U est solution de l'équation différentielle 4 tau² d2u sur dt2 plus 5 tau du sur dt plus U est égale à E. C'est une équation qui nous paraît bon, usuelle mais un peu complexe surtout quand on voit la tête du circuit juste ici. Et bien c'est justement les complexes qui vont nous permettre d'y arriver assez rapidement. Alors on sait que quand on utilise les complexes pour déterminer des relations entre deux différentes tensions on oublie la loi des mailles, on pense diviseur de tension. Bon si on fait un diviseur de tension pour la tension U on peut juste l'exprimer en fonction de cette tension qu'on va dire un peu intermédiaire ici. Mais ça tombe bien avec cette tension intermédiaire on pourra aussi l'exprimer en fonction de la tension de départ. Donc c'est comme ça qu'on va raisonner. Alors on commence par justement annoter cette tension intermédiaire U1 et bien c'est parti pour le diviseur de courant. La tension U c'est l'impellence complexe du condensateur sur la somme des impellences complexes juste ici. Donc c'est 1 sur Jc oméga le tout divisé par 1 sur Jc oméga plus 2R avec un grand R. Voilà fois la tension d'entrée U1. Très bien. Bon le réflexe c'est de multiplier en haut et en bas par Jc oméga pour nous séparer des deux délimiteurs qui sont un peu embêtants. Donc U c'est égal à 1 sur 1 plus 2Jrc oméga fois U1. Très bien ça c'est la première étape. Maintenant il faut appliquer le diviseur de tension pour déterminer U1 en fonction de E. Sauf que là on est embêté vu que on ne connaît pas trop l'impellence équivalente à tout ça. Il nous la faut pour appliquer le diviseur de courant. Donc on va déterminer cette impellence équivalente. Alors tout d'abord l'impellence équivalente à ces deux dipôles et bien ils sont en série donc par loi d'association c'est 2R plus 1 sur Jc oméga. Et ensuite ces deux branches sont ici pour déterminer l'impellence complexe de tout. Ces deux branches sont en dérivation donc c'est l'impellence complexe c'est Zx et Zc sur Zx plus Zc. On exprime les deux juste ici et en haut et en bas on multiplie par 2Jc oméga. Voilà c'est une transformation très courante de multiplier au numérateur et au délimiteur par la même expression. Donc ici ça va nous donner un facteur 1 ici, un facteur 2 là donc 3 plus 4Jrc oméga et puis on garde le facteur au numérateur. Ok donc c'est parti on peut écrire le diviseur de tension pour relier U1 à U2 et donc c'est égal à 2R plus 1 sur Jc oméga sur 3 plus 4Jrc oméga sur 2R plus 1 sur Jc oméga sur 3 plus 4Jrc oméga plus R. Très bien donc là vous avez compris la méthode classique c'est de multiplier en haut en bas par le délimiteur qui nous embête. Donc au numérateur on garde juste le facteur juste ici et puis qu'est ce que ça donne au délimiteur? Donc on a 3R qui vont apparaître qui vont s'additionner aux 2R qui sont juste ici donc ça vous donne bien 5R plus on a du 1 sur Jc oméga plus ce facteur fois R donc 4Jrc oméga. Très bien et finalement il y a toujours deux délimiteurs qui nous embêtent un peu donc on multiplie en haut et en bas par Jc oméga donc finalement ça nous donne 1 plus 2Jrc oméga sur 1 plus le J ici multiplié par J ça nous donne bien un moins donc moins 4R²C² oméga 2 et finalement plus 5Jrc oméga. Ok? Maintenant on n'a plus qu'à relier les deux tensions dont on disposait donc on a bien exprimé U1 en fonction de E et on avait U en fonction de U1 donc on peut exprimer juste ici U c'est sachant que on divisait seulement par 1 plus 2Jrc oméga et que c'est concrètement ce qu'on retrouve au numérateur ici et bien U c'est 1 sur 1 moins 4R²C² oméga 2 plus 5Jrc oméga fois E. Donc on a bien établi en complexe la relation entre U et E. Très bien mais en fait nous on nous demande une expression réelle c'est les signaux réels qui sont exprimés ici et en plus on demande tous les travaux qui sont faits sur U. On a la dérivée temporelle de seconde de U, la dérivée temporelle de U et U. Donc on va tout faire passer du même côté. Lorsqu'on multiplie U par ça, par ce numérateur, on a bien E qui est égal à 4T² en faisant apparaître T qui évoque Rc, 4T²J² oméga 2 U bar plus 5TJ oméga U bar plus U bar. Et là on a envie de revenir en réel pour exprimer les signaux réels. Comment ça se passe les différents facteurs pour repasser en réel? On se souvient que multiplier par J oméga en complexe, en réel ça revient à dériver. Je l'ai rappelé juste ici, on dispose de signaux complexes donc avec une amplitude complexe exponentielle de J oméga. Donc quand on dérive par rapport au temps, il y a bien un J oméga qui apparaît dans l'expression. Donc lorsque l'on repasse au réel, on a bien 4T² D2U sur DT2 plus 5T DU sur DT plus U qui est égal à E. On a effectivement obtenu l'équation différentielle que l'on souhaitait. Donc voilà c'est une méthode qui est assez simple puisqu'elle repose sur des diviseurs de courant. Au final dans les calculs il faut être à l'aise avec les manipulations de grandeur complexe mais on arrive à obtenir cette relation là mais aussi bien d'autres informations. C'est vraiment un exercice qui démontre la puissance de la résolution via les complexes et on peut obtenir des résultats d'électro-signétiques qu'on aurait pu déterminer via les lois de Baye mais de manière beaucoup plus simple. Voilà, merci beaucoup d'avoir suivi la vidéo et puis à bientôt!

Equation différentielle via les complexes

RELATED

Recommended videos

Association de dipôles

Créer un filtre

Filtre passe-haut RLC