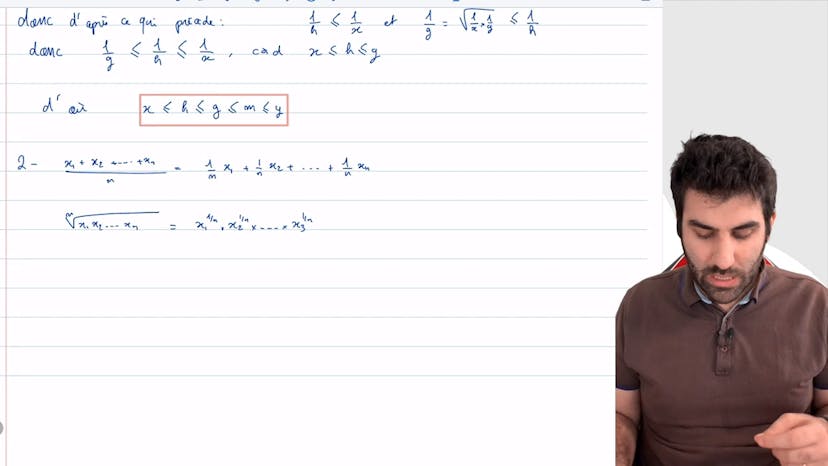All subjects
All subjects
 All subjects
All subjects
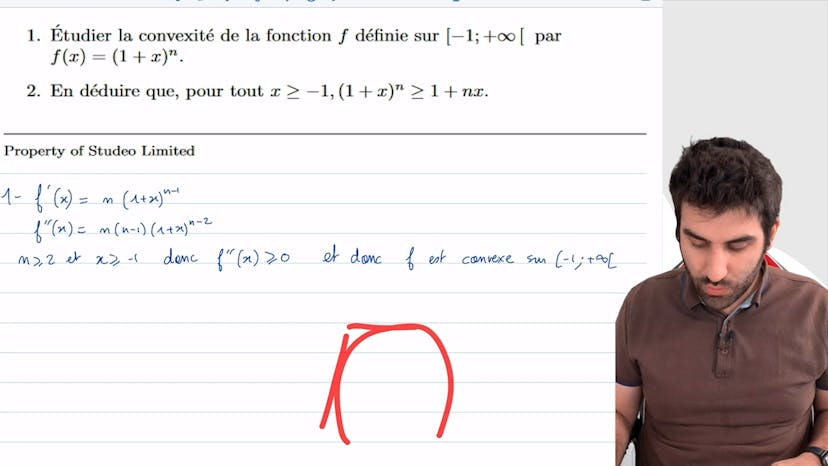
Majoration de f ’ grâce à f ”
Dans cet exercice, nous devons majorer une fonction de classe C2 par une autre fonction dépendant de M, le sup de la dérivée seconde sur AB. Pour justifier l'existence de M, nous utilisons l'hypothèse que F est de classe C2, ce qui signifie que la dérivée seconde est continue sur AB. Étant donné que la fonction est continue sur un segment, elle est bornée et atteint ses bornes. Par conséquent, le sup existe. On nous présente ensuite les fonctions G et H et on nous demande de montrer que G est convexe et H est concave. Pour cela, nous calculons les dérivées secondes de G et H et en étudions le signe. En utilisant la convexité de G et la concavité de H, nous déduisons une inégalité impliquant la valeur absolue de la dérivée de F. Enfin, nous regroupons les éléments pour obtenir l'inégalité finale de la valeur absolue de F.