Home

Terminale

Physique-Chimie

Physique

Lunette astronomique

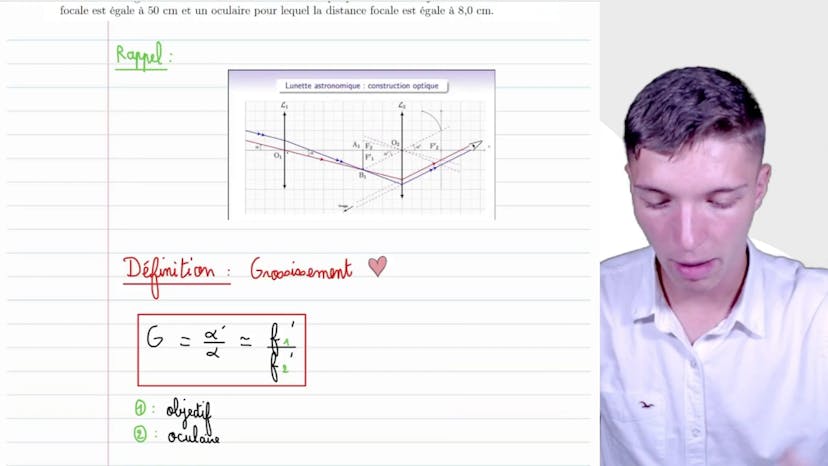
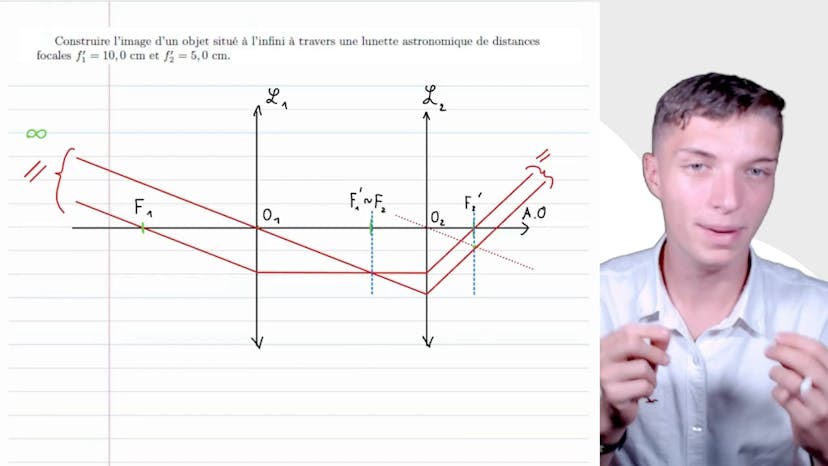
Dans cette vidéo, Matisse de Studio nous explique le principe du grossissement en optique. Il commence par rappeler que dans une lunette astronomique, il y a un objectif de distance focale f1 prime et un oculaire de distance focale f2 prime. La première étape est de schématiser la situation, en représentant les différents angles du trajet du rayon lumineux.

Ensuite, il montre comment, dans le cadre de petits angles, on peut démontrer que l'angle alpha est égal à a prime, b prime divisé par f1 prime, en utilisant la formule de la tangente. Il explique également que dans l'hypothèse des petits angles, la tangente de l'angle alpha est approximativement égale à l'angle lui-même.

Il montre ensuite comment, dans le même principe, on peut montrer que l'angle alpha prime est égal à a prime, b prime divisé par f2 prime, en utilisant à nouveau la formule de la tangente.

Enfin, il déduit le grossissement g, qui est égal à alpha prime sur alpha, en utilisant les résultats précédents. Il montre que le grossissement est égal à f1 prime divisé par f2 prime.

En résumé, Matisse explique le principe du grossissement en optique, en montrant comment les angles alpha et alpha prime sont liés à la distance focale de l'objectif et de l'oculaire, et comment cela permet de calculer le grossissement.

Bonjour à tous, c'est Matisse de Studio, et dans cette vidéo, on va démontrer la double expression pour le grossissement. Alors, on nous rappelle qu'une lunette astronomique est constituée d'un objectif de distance focale f1 prime et d'un oculaire de distance focale f2 prime. On note a prime, b prime, la taille de l'image intermédiaire. Il faut premièrement schématiser la situation. Alors, il s'agit du schéma classique, à savoir faire par cœur, les yeux bandés, ce que vous voulez. Donc, on le représente juste ici, avec les différents angles qui composent le trajet du rayon lumineux. Donc, on a bien sûr l'angle alpha, l'angle incident par rapport à l'axe pique, toujours arrivant sur l'objectif, et l'angle alpha prime, c'est l'angle du faisceau qui ressort. Et d'après la correspondance, on retrouve l'angle alpha juste ici, et l'angle alpha prime juste ici. C'est important pour la suite de l'exercice. Donc, c'est le même angle ici, ici, et puis ici, et ici. Très bien. Donc, à partir de là, question 2, dans le cadre de petits angles, montrer que alpha est égal à a prime, b prime divisé par f1 prime. Alors ça, il s'agit de la trigonométrie. Il faut donc relier alpha à f1 prime, donc o1 f1 prime, et a prime b prime. Donc, bien sûr, il faut utiliser ici la formule de la tangente, vu qu'il faut faire côté opposé sur côté adjacent. On a donc, dans le triangle de gauche, tangente de alpha, qui est égale à a prime b prime sur o1 f1 prime, qui est égale donc à a prime b prime divisé par f1 prime. Or, alors là, c'est la phrase très importante de l'exercice, dans l'hypothèse des petits angles, on a tangente de alpha qui est environ égale à alpha. C'est aussi le cas pour le sinus. Le sinus de alpha, quand alpha est très petit, est environ égal à alpha. On a donc alpha qui est égal à a prime b prime divisé par f1 prime. Troisième question, de même, montrer qu'alpha prime est égal à a prime b prime divisé par f2 prime. Et bien là, on va se placer dans le triangle de droite. On a la tangente de alpha de prime, c'est le côté opposé sur le côté adjacent. C'est donc a prime b prime divisé par f2 prime. Donc, quatrième question, on déduire le grossissement de g qui est égal à alpha prime sur alpha. Et donc, on déduire. Là, c'est le beau formule qu'on a appris par cœur, mais là qu'on redémontre. f1 prime divisé par f2 prime. Et donc, si on synthétise, on a alpha prime de ce côté-là, alpha juste ici. Donc, si on fait le rapport entre les deux, les deux a prime b prime se simplifient et on se retrouve avec f1 prime au numérateur et f2 prime au dénominateur, d'où l'expression de g. C'est alpha prime divisé par alpha et c'est égal à f1 prime divisé par f2 prime. Voilà, nous avons redémontré cette expression que nous avons utilisée tout au long de l'exercice. Donc, à partir de là, c'est bien de savoir la retenir et encore mieux de savoir la retrouver. C'est très satisfaisant. Merci beaucoup d'avoir suivi cette vidéo et puis je vous dis à bientôt. Sous-titrage ST' 501

Double expression

RELATED

Recommended videos

Grossissement

Schéma

Zoom