Online Physique-Chimie Courses by Top Instructors

Titane

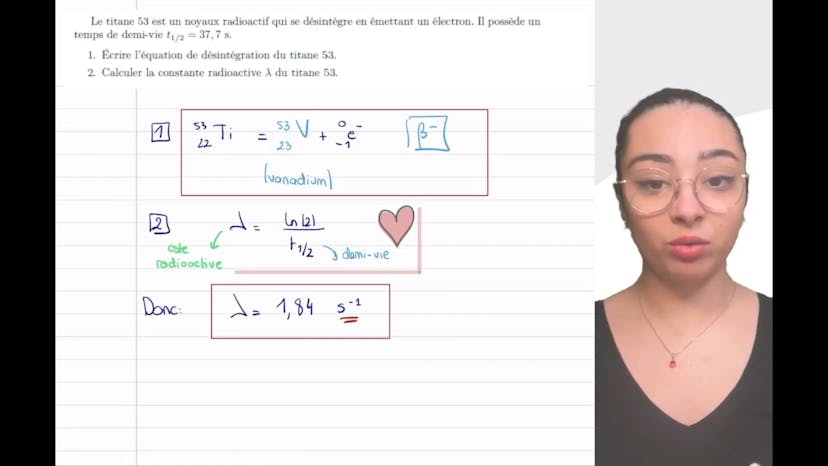
Aujourd'hui, nous allons parler du titane 53, un rayon radioactif qui se désintègre en émettant un électron. L'équation de désintégration est la suivante : titane 53 se désintègre en émettant un électron, ce qui donne du vanadium. Pour calculer la constante radioactive, nous utilisons la formule lambda = ln(2) / T1/2, où T1/2 est le temps de demi-vie du titane 53. En utilisant cette formule, nous obtenons une valeur de 1,84 avec l'unité en secondes^-1. Assurez-vous de bien utiliser les unités afin d'éviter des erreurs dans vos calculs. N'hésitez pas à poser vos questions en commentaire.

Activité radioactive

Aujourd'hui, je vais vous résumer un cours sur l'activité radioactive de manière SEO-friendly. Dans ce cours, nous étudions un échantillon de roche contenant du cobalt, bombardé artificiellement par des neutrons. L'objectif est de déterminer l'activité radioactive de cette roche. Pour cela, nous utilisons la formule de l'activité radioactive, A = λN, où A représente l'activité en becquerels (Bq), λ est la constante radioactive en secondes inverse, et N est le nombre de noyaux radioactifs à un certain instant. Nous disposons de deux instants différents pour lesquels nous connaissons le nombre de noyaux radioactifs. En utilisant la loi de décroissance radioactive, qui est une fonction exponentielle, nous pouvons lier ces deux valeurs. En isolant la constante radioactive λ, nous obtenons l'expression λ = 1/Tln(N₀/N), où T représente l'intervalle de temps entre les deux instants T₀ et T₁, N₀ est le nombre initial de noyaux radioactifs, et N est le nombre de noyaux restants à l'instant T₁. Ensuite, nous pouvons calculer l'activité radioactive à l'instant T₁ en multipliant λ par N₁, soit A(T₁) = λN₁. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions ou à laisser vos commentaires.

Décroissance radioactive

Aujourd'hui, nous avons analysé une courbe de décroissance radioactive d'un échantillon. Dans cet exercice, nous avons d'abord cherché à déterminer la durée au bout de laquelle 70% des noyaux radioactifs sont désintégrés. En utilisant la loi de décroissance radioactive, nous avons calculé que cette durée était d'environ 10 jours. Ensuite, nous avons estimé la durée au bout de laquelle il n'y aurait plus de noyaux radioactifs dans l'échantillon. Contrairement à une exponentielle continue, une exponentielle discrète, comme celle-ci, peut atteindre la valeur zéro. Nous avons donc cherché à déterminer à quel instant le dernier noyau se désintégrerait. En utilisant la formule ln(n₀/λ), où n₀ est le nombre initial de noyaux et λ est le paramètre de décroissance radioactive, nous avons calculé que cet instant correspondait à 80 jours. Enfin, nous avons exprimé cette durée en termes de demi-vie. Comme nous connaissions la demi-vie de l'échantillon (8 jours), nous avons converti les 80 jours en 10 demi-vies. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Uranium 238

Aujourd'hui, nous allons parler de l'uranium-238 et de son processus de désintégration. L'uranium-238 est un noyau radioactif qui se transforme en plomb-206, un noyau stable, par le biais de plusieurs étapes de désintégration. Ces désintégrations successives mènent à un noyau stable, conformément à la vallée de la stabilité dont nous avons parlé précédemment. La première étape de désintégration conduit à la formation de thorium-234. Il s'agit d'une désintégration radioactive de type alpha, comme le montre l'équation de réaction. Ensuite, le thorium-234 va à son tour se désintégrer, cette fois par une réaction de type bêta-, conduisant à la formation de protactinium-234. L'équation globale de toutes ces désintégrations successives nous permet de déterminer le nombre total de désintégrations radioactives nécessaires pour arriver au plomb-206, qui est considéré comme stable. En analysant l'équation, nous observons qu'il y a un nombre donné d'électrons et de désintégrations, ce qui indique que seules les réactions de type alpha et bêta- ont lieu. En comptant le nombre d'électrons et de particules alpha produits, nous pouvons déduire qu'il y a eu huit désintégrations alpha et six désintégrations bêta-. En additionnant ces deux chiffres, nous obtenons un total de 14 désintégrations avant d'atteindre le plomb-206, qui est stable. J'espère que ce cours vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Le terbium

Aujourd'hui, nous allons faire un exercice sur le terbium. Le terbium 152 est un métal malléable appartenant à la famille des lantanides. Il subit des désintégrations successives jusqu'à devenir stable. Un noyau radioactif est un noyau qui peut se désintégrer spontanément en libérant des particules et de l'énergie. Les désintégrations sont spontanées, ce qui signifie qu'elles se produisent sans aide extérieure. Pour cet exercice, nous devons écrire les équations de désintégrations successives du terbium 152 jusqu'à ce que le noyau final soit stable. Sur un graphique, nous sommes guidés par un code couleur indiquant les types de désintégrations (bêta moins, alpha, bêta plus et stable). En suivant ce code couleur, nous identifions chaque étape de désintégration du terbium 152 en galadium, puis en cérine et enfin en céréum 140, un noyau stable. Au total, il y a eu quatre désintégrations pour atteindre un noyau stable. N'hésitez pas à poser vos questions dans les commentaires.

Uranium 238 (2)

Dans cette vidéo, Leïla aborde le sujet de l'uranium 238 et son utilisation potentielle pour fabriquer des bracelets contenant des cristaux de roche en béphite. Elle se concentre sur la sécurité de ces bracelets radioactifs et propose un exercice pour mieux comprendre. Tout d'abord, elle demande de préciser la particule émise lors de la désintégration alpha de l'uranium. Elle explique qu'il s'agit d'un noyau d'hélium 4,2, également appelé particule alpha. Ensuite, Leïla explique qu'un bracelet de béphite peut contenir jusqu'à 2 mg d'uranium et demande de calculer le nombre de noyaux radioactifs correspondant. Pour cela, elle utilise des données de chimie générale, telles que la masse molaire et la constante lambda de l'uranium, afin de convertir la masse en nombre de noyaux. Elle présente deux formules importantes en chimie : n = petit m sur grand m et n = na. Ces formules permettent de convertir la masse en nombre de moles et le nombre de moles en nombre d'atomes. En utilisant ces formules, Leïla calcule que 2 microgrammes de roche contiennent 50,6 x 10^17 noyaux. Leïla aborde ensuite l'expression de l'activité d'un échantillon en fonction de la constante lambda et du nombre de noyaux. L'activité, notée a, est mesurée en becquerels (Bq), lambda est la constante de radioactivité et n est le nombre de noyaux. En utilisant les valeurs de lambda et de n obtenues précédemment, Leïla calcule que l'activité radioactive du bracelet est de 24,8 Bq. Elle souligne que cette activité est négligeable par rapport à d'autres sources de radioactivité présentes dans la vie quotidienne. Pour conclure, Leïla rappelle l'importance de comprendre que tout est radioactif dans la vie quotidienne, mais que cela n'est pas nécessairement dangereux tant que l'exposition reste en dessous d'une certaine dose maximale. Elle encourage les spectateurs à poser des questions ou à faire des commentaires.

Radioprotection

Dans cette vidéo, nous abordons le sujet de la radioprotection et comment protéger les individus lorsqu'ils sont en contact avec des matériaux radioactifs. Les méthodes pour se protéger des rayonnements ionisants comprennent trois points principaux : réduire la durée d'exposition aux rayons, s'éloigner de la source des rayonnements et utiliser un écran de protection pour bloquer les particules radioactives. Un tableau est présenté pour illustrer la couche de demi-atténuation, qui est l'épaisseur nécessaire pour diviser par deux le flux de rayons gamma et antara. Le plomb est souvent utilisé en radioprotection car il nécessite une épaisseur minimale pour réduire efficacement le flux de rayons gamma. Par exemple, l'utilisation de plomb nécessite 15 cm d'épaisseur pour absorber la moitié des rayons ionisants, tandis que l'aluminium ne nécessite que 5 cm. Il est important de se souvenir de ces chiffres car ils sont utiles dans l'analyse de documents et d'autres contextes scolaires. N'hésitez pas à poser vos questions en commentaire.

Demi-pile

Dans cette vidéo, Matisse de Studio explique le concept de demi-pile en chimie des solutions. Une demi-pile est un système chimique composé d'une électrode, d'un électrolyte, et met en contact le réducteur et l'oxydant d'un couple oxido-réducteur. Pour déterminer si un système peut correspondre à une demi-pile, il faut vérifier plusieurs critères. Dans le premier cas présenté, on a une électrode en cuivre qui peut conduire les électrons, ainsi qu'un électrolyte qui est probablement de l'eau. De plus, une réaction d'oxydo-réduction peut se produire avec l'électrode de cuivre, ce qui confirme que ce système peut correspondre à une demi-pile. Dans le deuxième cas, on retrouve une électrode en platine et un électrolyte. Le couple oxydo-réducteur Fe3+/Fe2+ est présent et une demi-réaction d'oxydo-réduction peut se produire. Donc, ce système peut également correspondre à une demi-pile électrochimique. En revanche, dans le dernier cas, bien qu'on ait une électrode en platine et un électrolyte, les espèces présentes correspondent à un acide et à sa base conjuguée. Il n'y a pas de réaction d'oxydo-réduction possible, donc ce système ne peut pas correspondre à une demi-pile. En conclusion, il est important de connaître la définition d'une demi-pile pour identifier si un système chimique peut correspondre à cette notion. Cela permet de mieux comprendre comment se met en place une réaction d'oxydo-réduction.

Quotient de réaction

Aucun résumé n'est disponible pour cette vidéo

Equation de fonctionnement

Aucun résumé n'est disponible pour cette vidéo

Equation et quotient

Dans cette vidéo, Mathis explique comment déterminer des équations de réaction à partir des quotients de réaction. Le quotient de réaction est un outil très intéressant car il renferme beaucoup d'informations sur la réaction étudiée. Pour la première équation, on observe que la concentration de NH4+ est élevée à la puissance 1, ce qui indique que NH4+ est un produit de la réaction avec un coefficient stoichiométrique de 1. De même, F- est un produit de réaction avec un coefficient de 1. Au dénominateur, on retrouve HF et NH3, qui sont donc les réactifs. Ainsi, l'équation de réaction est NH3 + HF -> NH4+ + F-. Pour la deuxième équation, on remarque que le produit de la réaction est AGCN2-, correspondant au complexe de Lyon-Argent. Les réactifs sont AG+ et CN2-, avec un coefficient stoichiométrique de 2 devant CN-. Ainsi, l'équation de réaction est AG+ + 2CN- -> [AGCN]2-. Il est important de ne pas intervertir les réactifs et les produits dans l'équation. Les espèces mentionnées dans les équations sont toutes en solution. En conclusion, les quotients de réaction peuvent servir à déterminer les équations de réaction. C'est un outil très utile pour l'étude des réactions chimiques. Merci d'avoir suivi cette vidéo et à bientôt !