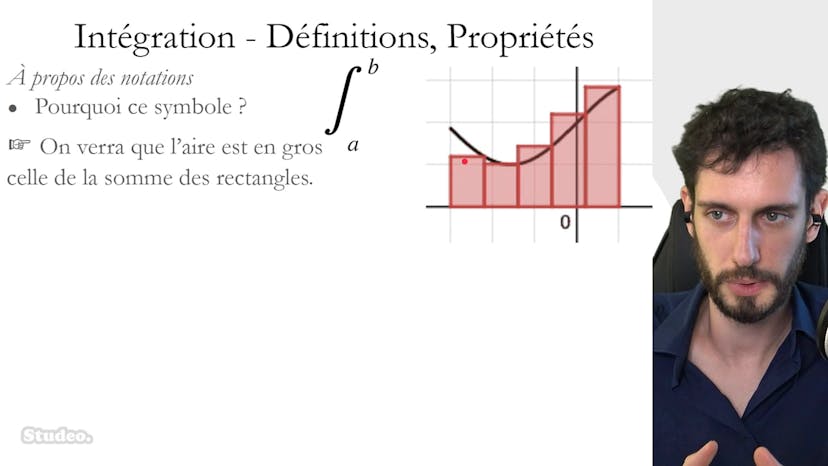
Méthode des Rectangles

Dans ce cours, nous apprenons à calculer une aire géométrique à l'aide de la méthode des rectangles. La courbe intégrée n'a pas une forme géométrique simple, donc nous ne pouvons pas calculer l'aire de manière directe. Cependant, nous pouvons encadrer cette aire en utilisant des petits rectangles en dessous de la courbe et des grands rectangles au-dessus. En diminuant la largeur des rectangles, nous affinons notre encadrement et nous tendons vers l'aire recherchée, c'est-à-dire l'intégrale. Nous cherchons donc à encadrer l'aire sous la courbe de la fonction de 0 à 4. La fonction est croissante, donc nous encadrons l'aire en utilisant les rectangles a'0, a'1, a'2 et a'3. Les a'0, a'1, a'2 et a'3 se calculent en multipliant la largeur par la hauteur de chaque rectangle. Par exemple, a'1 est égal à 1 fois 1 (largeur fois hauteur), ce qui donne 1. En utilisant ces calculs, nous obtenons l'encadrement 1 plus racine de 2 plus racine de 3 pour l'aire sous la courbe, et 3 plus racine de 2 plus racine de 3 pour l'encadrement formé par les petits rectangles. Pour augmenter la précision de l'encadrement, nous pouvons utiliser des rectangles de largeur plus petite, comme 1,5, 1,25, etc. En faisant tendre la largeur vers zéro, nous obtenons des rectangles qui collent de plus en plus à la courbe et ainsi un encadrement plus précis. En résumé, la méthode des rectangles permet d'encadrer l'intégrale lorsque nous ne pouvons pas trouver une primitive de la fonction. Il est possible d'améliorer la précision de l'encadrement en utilisant des rectangles de plus en plus petits.