Méthode des Rectangles

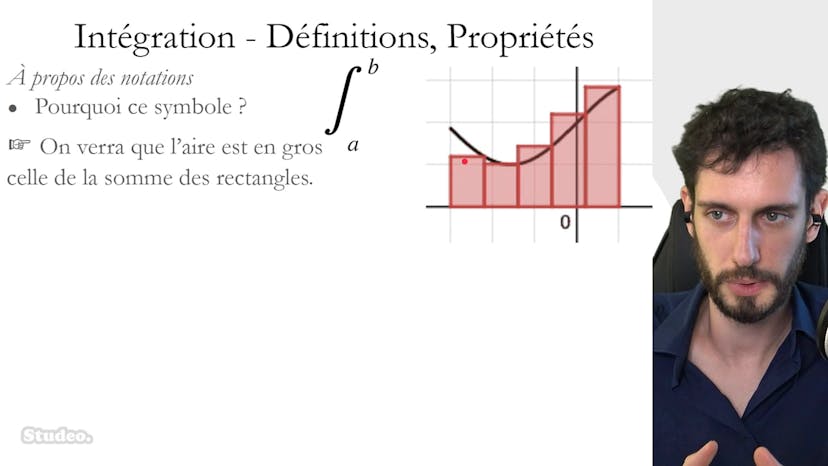
Ce cours traite de la méthode d'encadrement pour calculer une intégrale. L'objectif est d'estimer l'aire sous une courbe qui n'a pas une forme géométrique simple en utilisant la méthode des rectangles. Cette méthode consiste à encadrer l'aire totale par l'aire des petits rectangles situés en dessous de la courbe et par l'aire des grands rectangles situés au-dessus de la courbe. En diminuant la largeur des rectangles, on affine progressivement l'encadrement et on tend vers l'intégrale recherchée. Cette méthode est appelée l'intégrale de Riemann. Dans cet exemple, on cherche à encadrer l'aire sous la courbe d'une fonction croissante entre 0 et 4. On divise l'intervalle en petits rectangles et on calcule l'aire de chacun en multipliant la largeur par la hauteur. En utilisant la fonction racine carrée, on obtient les aires des différents rectangles : a'1 = 1, a'2 = √2, a'3 = 2. On peut ensuite encadrer l'intégrale en additionnant ces aires : 1 + √2 + √3 < intégrale < 3 + √2 + √3. Cet encadrement n'est pas très précis car il y a une différence de 2 entre les bornes supérieure et inférieure. En augmentant la précision en utilisant des rectangles de largeur plus petite (par exemple, 1,5 au lieu de 1), on obtient un encadrement plus fin qui se rapproche davantage de l'intégrale réelle. En résumé, la méthode d'encadrement permet d'estimer l'intégrale d'une fonction en utilisant la somme des aires des rectangles situés en dessous et au-dessus de la courbe. En affinant la précision en diminuant la largeur des rectangles, on obtient un encadrement de plus en plus précis de l'intégrale. C'est une méthode utile lorsque l'on ne peut pas trouver une primitive de la fonction.