Introduction Limites

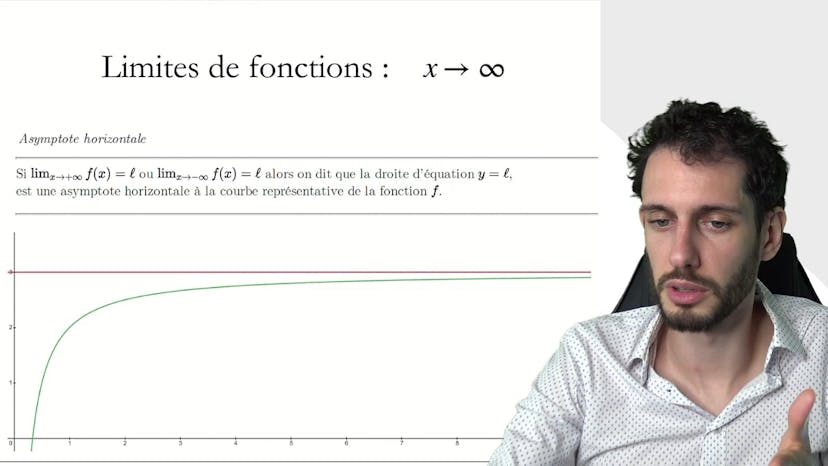
Lorsqu'on étudie les limites de fonctions, on peut s'inspirer de ce qu'on a vu sur les suites. Les suites sont des fonctions qui portent uniquement sur les entiers, tandis que les fonctions sont plus génériques et se portent sur l'ensemble des réels. Ainsi, on peut parler de limites en l'infini et en un réel. Il y a aussi des cas où il n'y a pas de limite, par exemple lorsque la fonction oscille à l'infini. Dans le cas où la limite existe, la fonction peut se rapprocher d'une valeur réelle ou tendre vers plus ou moins l'infini. On peut illustrer ces cas avec des graphes. Dans cette vidéo d'introduction, nous aborderons ces différents cas et introduirons la notion d'asymptote. En résumé, il faut connaître les définitions et les exemples de limites, ainsi que les méthodes d'analyse graphique et de calcul des limites. N'hésitez pas à poser des questions et interagir avec les autres membres dans la FAQ.