Déf formelle

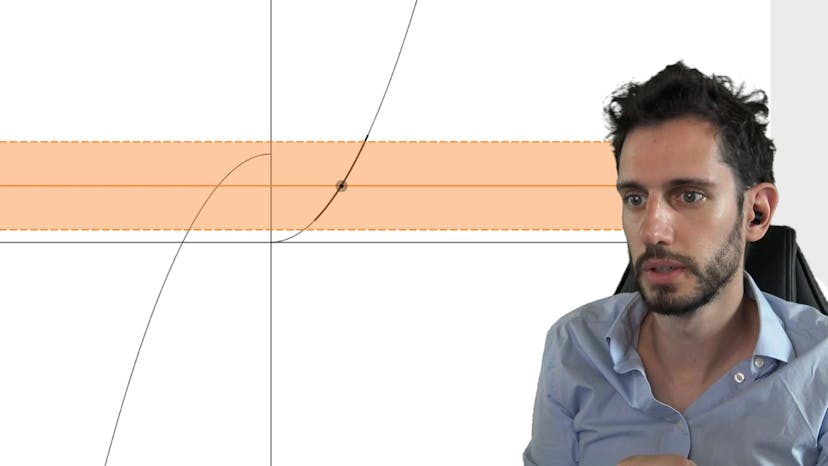
La continuité en mathématique fait référence à la propriété d'une fonction où il n'est pas nécessaire de lever le stylo pour la tracer. De manière formelle, une fonction f est continue en un point a si et seulement si la limite finie de f lorsque x tend vers a est égale à f(a). Si cette condition est vérifiée pour tous les points d'un intervalle, on dit que la fonction est continue sur cet intervalle. La limite finie en un point signifie que lorsque x approche d'une valeur a, la fonction se rapproche d'une valeur l. Pour vérifier cela, on peut sélectionner un intervalle orange arbitraire et trouver un intervalle bleu correspondant où toutes les valeurs de la fonction sont comprises dans l'intervalle orange. Si cette condition est vérifiée pour tous les intervalles orange de tailles différentes, alors la fonction a une limite finie en un point. La continuité d'une fonction est établie lorsque la limite finie en un point est égale à f(a).