Fonctions usuelles

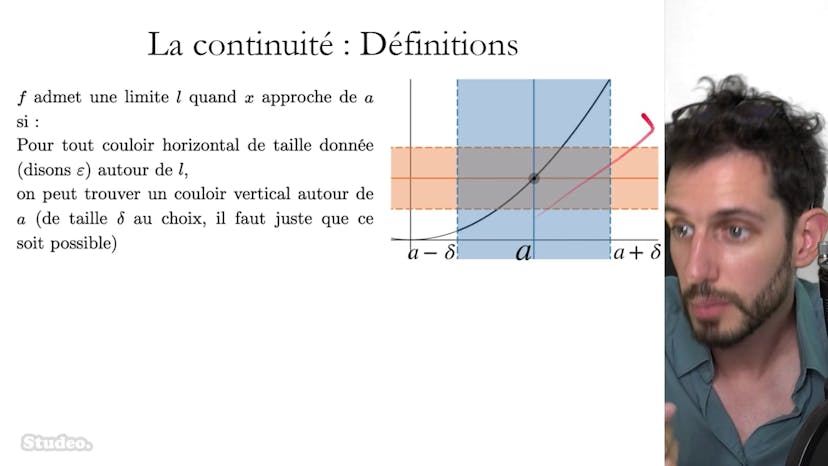
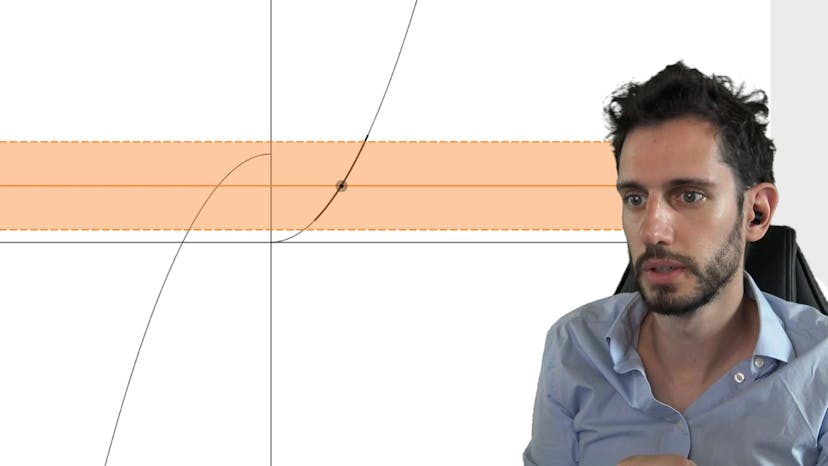
Ce cours traite de la continuité des fonctions visuelles. Il explique que la plupart des fonctions visuelles rencontrées depuis le lycée sont continues, y compris les fonctions x puissance n, 1 sur x, racine carrée, valeur absolue, exponentielle, sinus et cosinus, ainsi que toutes les fonctions construites à partir de combinaisons de celles-ci. Les fonctions non continues sont généralement des fonctions construites par morceaux et par branches. Le cours rappelle également les différents types de discontinuité, tels que la discontinuité par définition, les sauts de discontinuité, les discontinuités prolongeables et les discontinuités en un point mal placé non-prolongeables. Il souligne également que l'ensemble de définition, l'ensemble de continuité et l'ensemble de dérivabilité ne sont pas nécessairement les mêmes pour une fonction donnée. Par exemple, la fonction valeur absolue de x est définie sur R, continue sur R mais non dérivable sur R. Cependant, elle est dérivable sur R étoile. Le cours se termine en encourageant les questions dans le forum et annonce une prochaine vidéo.