Discontinuités : exemples

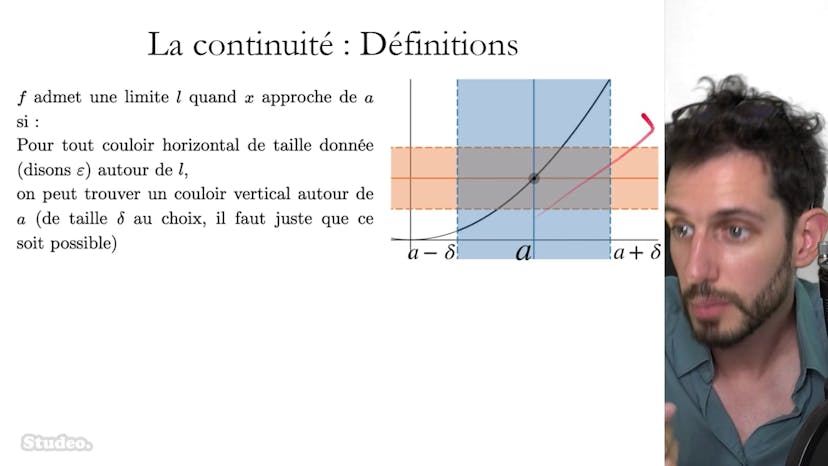
La continuité d'une fonction est définie comme étant la présence d'une limite finie en un point, qui est également la valeur de la fonction à ce point. Si pour un couloir horizontal donné, il est possible de trouver un couloir vertical dans lequel toutes les valeurs de la fonction se trouvent également dans le couloir horizontal, alors la fonction est continue. Par exemple, si le couloir orange est suffisamment réduit, toutes les valeurs de la fonction se trouvent dans ce couloir, ce qui signifie que la fonction se rapproche infiniment du point au milieu. Cependant, il existe également des discontinuités dans les fonctions. La première est la discontinuité par non-existence du point, ce qui signifie que le point n'est pas défini. Par exemple, la fonction f(x) = 1/x n'est pas définie en zéro, ce qui rend la fonction non continue en zéro. En plus de cela, la fonction a un comportement croissant à l'infini à droite et décroissant à l'infini à gauche. Un autre exemple de discontinuité est une fonction composée de deux paraboles, où la valeur de la fonction est zéro en zéro pour la branche de droite, mais n'est pas attribuée à la branche de gauche. Cela crée un saut dans la fonction, ce qui la rend discontinue. Enfin, il y a des discontinuités rattrapables, où la fonction n'est pas définie en un point, mais il est possible de trouver une valeur pour ce point qui permettrait de rendre la fonction continue. Par exemple, la fonction f(x) = sin(x)/x n'est pas définie en zéro, mais si on attribue une valeur de 1,7 à ce point, la fonction peut être prolongée de manière continue. En somme, la continuité d'une fonction se base sur la présence d'une limite finie en un point, tandis que les discontinuités peuvent être dues à la non-définition d'un point, à des sauts ou peuvent être rattrapables en attribuant une valeur spécifique au point.