Démo inégalité convexité

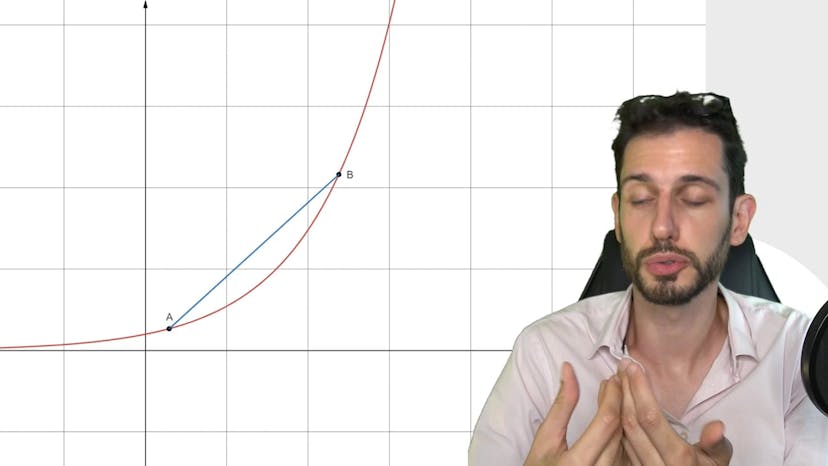
Dans ce cours, nous prenons les points réels X et Y, ainsi que les points associés A et B. Nous avons une séquence illustrée par un dessin, ainsi qu'un point M défini par les coordonnées Apcis (TX+1-TY) et (TF2X+1-TF2Y). Nous allons démontrer que cette ordonnée est bien sur la séquence. Pour cela, nous analysons la position de l'apcis entre X et Y, ainsi que l'ordonnée entre TF2X et TF2Y, afin de montrer qu'elle est bien sur la séquence. Nous démontrons aussi que M appartient au segment AB en vérifiant que les Apcis de M et de Y sont comprises entre les Apcis de A et B. Ensuite, nous vérifions que M est sur la droite AB en utilisant l'équation de la droite, où Y est égal à AlphaX+Beta. Nous calculons Alpha en utilisant les variations des ordonnées et des Apcis entre A et B, et nous trouvons Beta en utilisant le fait que le point A est sur la droite. Pour vérifier que M est sur la droite, nous remplaçons l'apcis de M à la place de X dans l'équation et espérons obtenir l'ordonnée de M à la fin du calcul. En effectuant les calculs, nous trouvons que l'apcis de Y correspond à l'ordonnée de M, ce qui confirme que M est sur la droite. En conclusion, en démontrant que M appartient au segment AB qui est sur la séquence CF, nous pouvons affirmer que l'image de l'apcis de M par la séquence est au-dessus de son image par F.