Des inégalités classiques

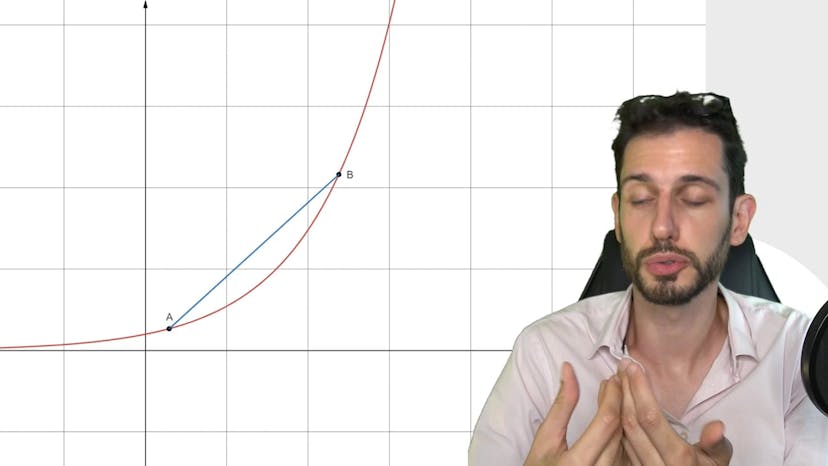
Dans cet exercice, on utilise la convexité et la concavité pour démontrer certaines inégalités. Tout d'abord, on démontre que pour tout réel X, l'exponentielle de X est supérieure à 1 + X, et même si X est non nul, l'inégalité est stricte. Pour cela, on remarque que 1 + X peut être vu comme l'exponentielle de 0 fois X + l'exponentielle de 0. On reconnaît alors l'équation de la tangente à la courbe de l'exponentielle de X au point (0,1). Comme l'exponentielle de X est strictement convexe, la courbe est au-dessus de cette tangente, et donc E(X) est supérieur ou égal à 1 + X pour tout X réel. Si X est différent de 0, alors E(X) est strictement plus grand que 1 + X. Ensuite, on démontre que le logarithme de (1 + X) est inférieur ou égal à X. On remarque que le coefficient directeur de la tangente à la courbe de log(1 + X) en 0 est 1, donc la dérivée de log(1 + X) est égale à 1 / (1 + X), et elle vaut 1 lorsque X = 0. Donc l'équation de la tangente en 0,0 est Y = X. En étudiant la convexité de la fonction log(1 + X), qui est strictement concave, on peut conclure que la courbe est en-dessous de cette tangente, ce qui démontre l'inégalité recherchée. Enfin, on cherche à encadrer sin(X) entre pi/2 et 0 pour X dans l'intervalle [0, pi/2]. On montre que sin(X) est concave dans cet intervalle en calculant sa dérivée seconde qui est -sin(X), et qui est donc négative dans cet intervalle. On démontre ensuite que sin(X) est inférieur ou égal à X en montrant que X est l'équation de la tangente à la courbe de sin(X) en 0. Finalement, on montre que sin(X) est supérieur ou égal à pi/2 en trouvant une corde entre les points (0,0) et (pi/2,1), qui est une droite décroissante. Le maximum de cette droite est atteint en X = 0, et vaut pi/2, ce qui démontre l'encadrement recherché.