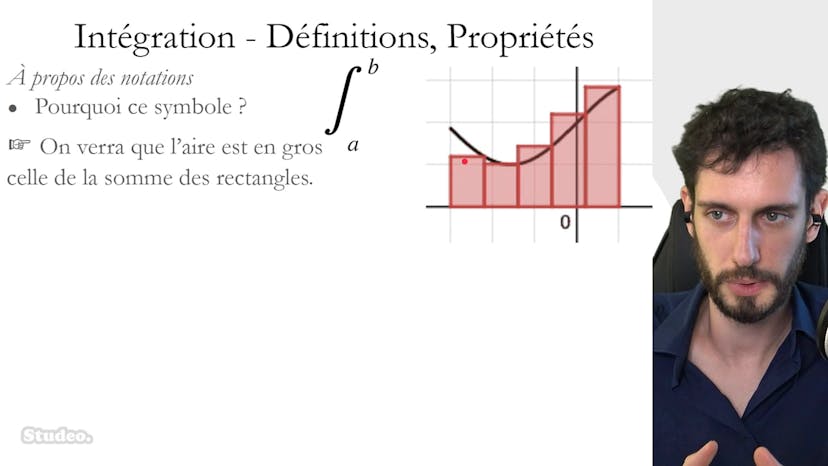
Intégrale et Aire

Lorsque nous souhaitons calculer une intégrale de façon géométrique, sans utiliser une fonction, il est important que la forme géométrique soit « simple ». Dans cet exemple, nous avons une fonction affine pour laquelle l'erreur d'intégration correspond à un trapèze. Nous nous intéressons ici à l'intégrale de la fonction x plus 2 entre -0,5 et 2. Nous pouvons représenter cette intégrale comme l'erreur sous la courbe jusqu'à l'axe des abscisses. Il existe deux méthodes pour calculer cette intégrale. La première consiste à calculer la primitive de x plus 2 et à effectuer les calculs habituels. La seconde méthode consiste à réaliser un calcul géométrique de l'erreur, étant donné que celle-ci correspond à un trapèze. Dans cette dernière méthode, nous devons déterminer la hauteur, la largeur et la longueur des bases du trapèze. Pour trouver ces informations, nous avons choisi de trouver les coordonnées des points a, b, c et d. Les points a et b se trouvent sur la droite de la fonction et vérifient donc son équation. Nous connaissons les abscisses : xa est égal à -0,5 et xb est égal à 2. Pour trouver les ordonnées respectives de ces points, nous utilisons l'équation de la droite, à savoir y = x + 2. Ainsi, si xa vaut -0,5, nous avons ya = -0,5 + 2, ce qui donne 1,5. Les coordonnées de a sont donc (-0,5 ; 1,5). De manière similaire, si xb vaut 2, nous avons yb = 2 + 2, soit 4. Les coordonnées de b sont donc (2 ; 4). En ce qui concerne les points c et d, ils se trouvent sur l'axe des abscisses et leurs coordonnées sont respectivement (2 ; 0) et (-0,5 ; 0). Nous devons maintenant calculer les différentes longueurs des côtés du trapèze. Comme il s'agit de lignes horizontales ou verticales, cela est relativement simple. Pour les côtés a et d, nous faisons la différence entre les ordonnées de a et d, ce qui donne 1,5. Pour les côtés b et c, nous faisons la différence entre les ordonnées de b et c, ce qui donne 4. Pour les côtés d et c, nous faisons la différence entre les abscisses de c et d, ce qui donne 2,5. En utilisant la formule de l'aire du trapèze, qui est la moyenne des deux bases multipliée par la hauteur, nous pouvons alors calculer l'aire de notre trapèze. Dans notre cas, cela donne (1,5 + 4) * 2,5, ce qui équivaut à 6,875. La formule de l'aire du trapèze dépend de la définition des bases et de la hauteur, mais peu importe la définition choisie, il s'agit de la moyenne des deux côtés parallèles de longueurs différentes, multipliée par la base. Dans notre exemple, nous l'avons vu comme la base multipliée par la moyenne des hauteurs. Ainsi, nous avons présenté un cas particulier où il n'est pas nécessaire de calculer les primitives de la fonction pour obtenir l'intégrale, mais il est possible d'utiliser le calcul direct de l'aire géométrique, en l'occurrence ici, du trapèze. C'est une méthode alternative pour calculer une intégrale en se basant sur une approche géométrique.