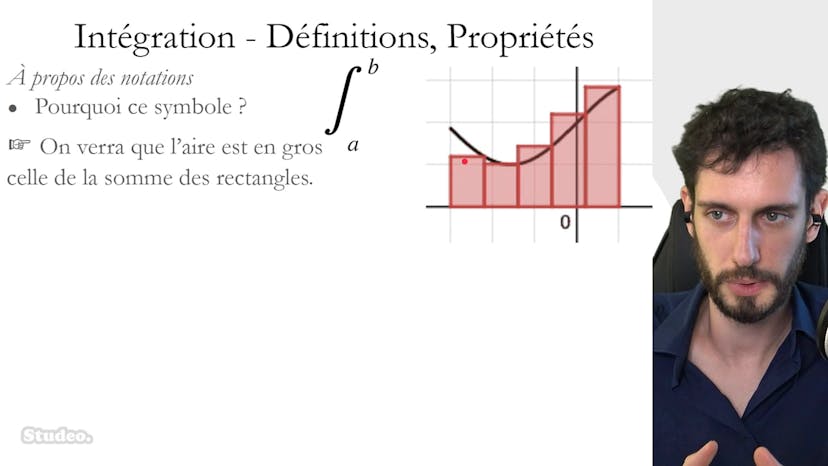
Méthode des Rectangles

L'intégrale de Riemann est une méthode utilisée pour calculer des aires sous des courbes géométriques complexes. Elle consiste à encadrer cette aire en utilisant la méthode des rectangles. Dans cette vidéo, la courbe intégrée n'a pas une forme géométrique simple, ce qui rend difficile le calcul direct de l'aire. Cependant, en utilisant la méthode des rectangles, il est possible de l'encadrer. L'idée est de diviser l'aire totale en petits rectangles, en choisissant une largeur appropriée. On peut ainsi obtenir une approximation de l'aire sous la courbe en sommant les aires des petits rectangles. L'encadrement obtenu sera moins précis si la largeur des rectangles est plus grande, et plus précis si la largeur est plus petite. En augmentant la précision, on se rapproche de l'aire réelle sous la courbe. Dans l'exemple donné, l'objectif est d'encadrer l'aire sous la courbe de 0 à 4. La courbe est croissante et la fonction f(y) est connue (racine de x). En calculant les aires des petits rectangles, on obtient un encadrement de cette intégrale. Il est possible d'améliorer la précision de l'encadrement en diminuant la largeur des rectangles. En faisant tendre cette largeur vers zéro, les rectanglres se rapprochent de la courbe géométrique, et l'encadrement devient plus précis. Il est à noter que cette méthode d'encadrement est utilisée lorsqu'on ne peut pas trouver une primitive de la fonction pour calculer directement l'intégrale. En conclusion, l'intégrale de Riemann est une méthode permettant de calculer des aires sous des courbes géométriques complexes en utilisant la méthode des rectangles. L'encadrement obtenu dépend de la largeur des rectangles et peut être amélioré en diminuant cette largeur.