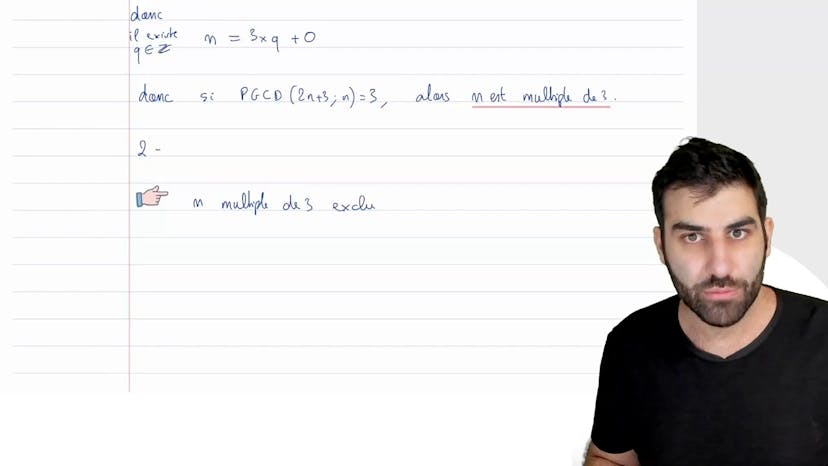PGCD et Suite

Dans cet exercice, on nous parle de deux suites : u et v. La suite u est définie par u0 = 0, u1 = 1, et la relation de récurrence un+2 = 3un+1 - 2un. La suite v est définie par vn = un+1 - un. On nous demande de montrer que la suite v est une suite géométrique et de déterminer sa raison et son premier terme. Pour montrer que la suite v est géométrique, on calcule vn+1 et on essaye de l'écrire comme quelque chose fois vn. En effectuant les calculs, on obtient que vn+1 = 2vn. Donc la suite v est bien géométrique avec une raison de 2 et son premier terme est v0 = 1. Ensuite, on nous demande de déduire que pour tout entier n, un est un entier naturel et que un+1 = 2(un+1). Cette question peut sembler étrange car on parle de la suite v et ensuite on demande de déduire quelque chose à partir de cette question. Cependant, on remarque que la suite v est construite de manière particulière : vn est la différence entre deux termes consécutifs de la suite u. On peut donc penser à une somme télescopique pour trouver des informations sur un et un+1. En effectuant la somme des termes de la suite v, on obtient que la somme de vn pour k allant de 0 à n est égale à un+1. Or, la suite v étant géométrique, on connaît une formule pour calculer la somme d'une suite géométrique : v0(1-q^n+1)/(1-q), où v0 est le premier terme de la suite v, q est la raison et n est le nombre de termes. En remplaçant par les valeurs connues, on trouve que la somme des termes de v est égale à 2^(n+1) - 1. Donc un+1 = 2^(n+1) - 1. Cela signifie que pour tout entier naturel n, un est un entier. On nous demande également de vérifier que un+1 = 2un+1. En substituant un par 2^(n+1) - 1 dans cette équation, on obtient bien l'égalité. Enfin, on déduit que deux termes consécutifs de la suite u sont premiers entre eux. Pour le prouver, on utilise le théorème de Bézout qui dit qu'une combinaison linéaire de deux entiers donne le PGCD de ces entiers. On a montré précédemment que un+1 = un - 2un. Donc en passant un+1 de l'autre côté de l'équation, on obtient que le PGCD de un et un+1 est égal à un. Donc les termes consécutifs de la suite u sont bien premiers entre eux.