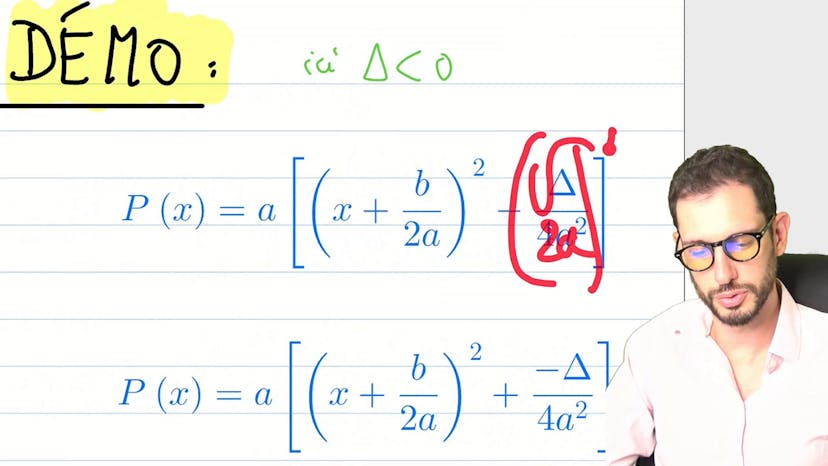Rappel : le conjugué

Le cours traite du concept de conjugué d'un nombre complexe. Le conjugué de z = a + ib est noté z-bar et égal à a - ib. Le cours explique les propriétés du conjugué, à savoir que le conjugué de la somme de deux nombres complexes est égal à la somme des conjugués, que le conjugué du produit de deux nombres complexes est égal au produit des conjugués, et enfin que le conjugué du quotient de deux nombres complexes est égal au quotient des conjugués. 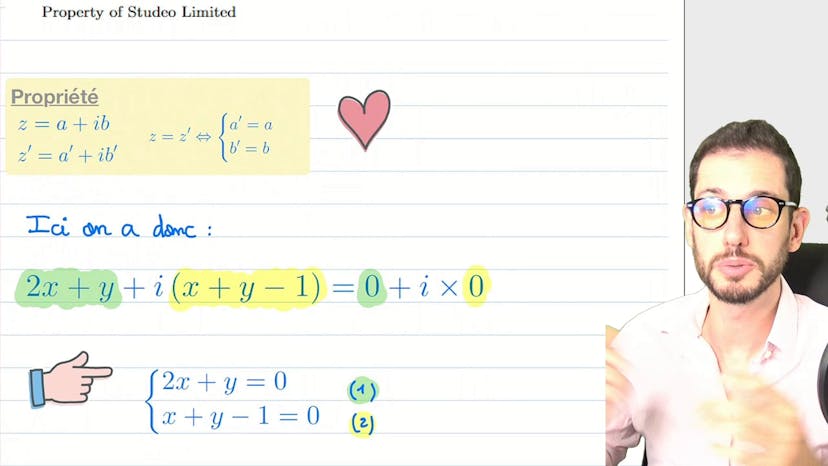Ensuite, le cours présente une équation à résoudre pour z, en utilisant le concept de conjugué. Pour cela, il introduit a et b tel que z = a + ib, et à partir de là, il effectue des calculs pour identifier les parties réelles et imaginaires de l'équation, ce qui permet de résoudre pour a et b et de trouver la solution. Le cours conclut en soulignant qu'il existe d'autres astuces plus avancées pour résoudre ces équations, mais la méthode basique de l'introduction de a et b reste valide et simple à utiliser. Le cours invite les étudiants à poser des questions et se termine en annonçant la prochaine vidéo.