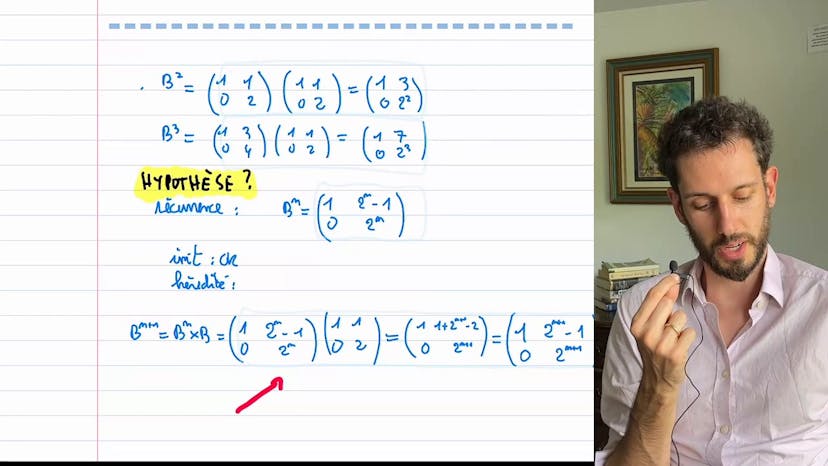Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Arithmétique dans Z
- Structures Algébriques
- Calcul matriciel et systèmes
- Espaces Vectoriels
- Matrice 2ième Partie
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Arithmétique dans Z
- Structures Algébriques
- Calcul matriciel et systèmes
- Espaces Vectoriels
- Matrice 2ième Partie
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Puissance nième Polynome annulateur
Dans ce cours, on étudie la division euclidienne du polynôme x^n par le polynôme x^2 - 3x + 2. Pour calculer le polynôme reste R2x, on utilise les racines x=1 et x=2 du polynôme diviseur pour éliminer le terme Q2x dans l'équation. On obtient ainsi le polynôme reste R2x qui est de degré 1 et peut s'écrire sous la forme AX + B. En résolvant les équations, on trouve que B=2^n et A=2^n-1. Le polynôme reste R2x peut donc s'écrire comme 2^n-1 * (x-2) + 2^n.
Ensuite, on applique cette structure polynomiale à une matrice A. En remarquant que A^2 - 3A + 2I = 0, on déduit que A^n = R2A. Ainsi, on peut calculer A^n en utilisant le polynôme reste R2A qui s'écrit comme 2^n-1 * (A-2I) + 2^n * I.