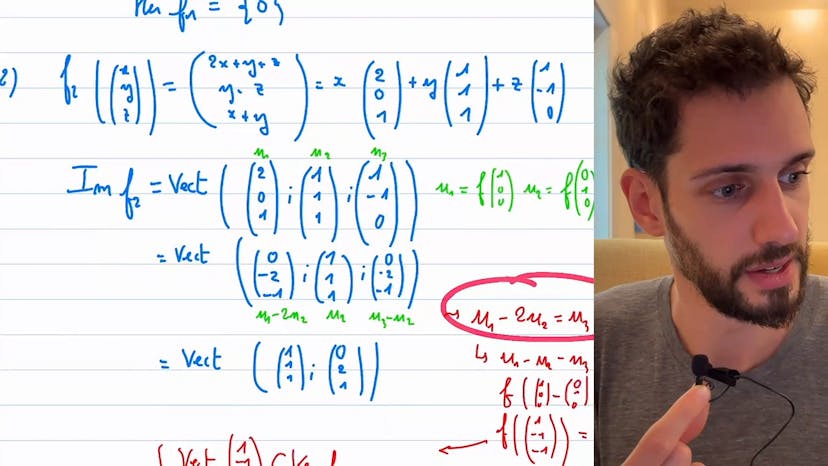Noyau et image

Dans cet exercice, nous étudions les applications linéaires dans l'espace des polynômes de degré n. Il est important de noter que cet espace a une dimension de n+1, contrairement à ce que l'on pourrait croire. La base de cet espace est composée des polynômes de degré n, n-1, 1 et 0. Dans cet exercice, nous avons une application linéaire définie par phi(p) = p(x+1) - p(x). Pour vérifier que c'est un endomorphisme, il faut montrer que c'est linéaire et que l'image de phi est incluse dans E. Pour la linéarité, on peut simplement le mentionner car c'est évident puisque tout est défini avec des signes moins. Pour montrer que l'image de phi est incluse dans E, on calcule phi(xi) et on utilise le binôme de Newton. On trouve que l'image de phi est incluse dans l'ensemble des polynômes de degré n-1. Ensuite, on s'intéresse à l'égalité de phi au carré, c'est-à-dire phi². On remarque que l'image de phi n'est pas égale à l'espace E, mais elle est incluse dans E. Les polynômes de degré n ne sont jamais atteints par phi. Il est important de ne pas commencer par résoudre phi², mais plutôt d'étudier l'image de phi, car cela peut simplifier les choses. On utilise le théorème de Durand, qui dit que la dimension de l'image de phi plus la dimension du noyau de phi équivaut à la dimension de l'espace de départ. Dans notre cas, la dimension de l'image de phi est n-1 et la dimension de l'espace de départ est n+1. Donc la dimension du noyau de phi est de 1. En utilisant l'astuce que si deux espaces ont la même dimension et que l'un est inclus dans l'autre, alors ils sont égaux, on peut conclure que le noyau de phi est égal à l'espace E. En résumé, dans cet exercice, nous avons étudié une application linéaire dans l'espace des polynômes de degré n. Nous avons montré qu'elle est linéaire et que son image est incluse dans l'ensemble des polynômes de degré n-1. De plus, nous avons utilisé le théorème de Durand et l'astuce de la dimension pour montrer que le noyau de l'application est égal à l'espace E.