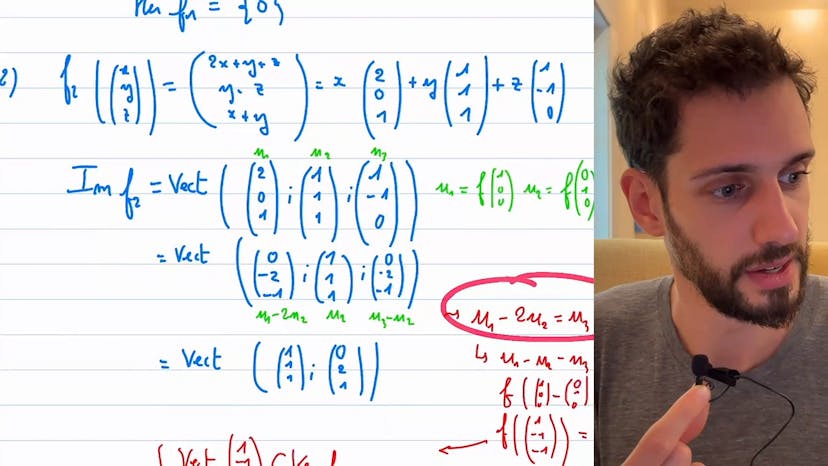Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Arithmétique dans Z
- Structures Algébriques
- Calcul matriciel et systèmes
- Espaces Vectoriels
- Matrice 2ième Partie
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Arithmétique dans Z
- Structures Algébriques
- Calcul matriciel et systèmes
- Espaces Vectoriels
- Matrice 2ième Partie
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Théorème du rang
Dans cet exercice, on considère un espace vectoriel E de dimension finie et deux endomorphismes F et G qui vérifient les équations E = kref + krg et E = imef + img. L'objectif est de montrer que les sommes sont directes, c'est-à-dire qu'il n'y a aucun élément commun à part 0.
Pour résoudre cet exercice, on utilise le théorème du rang qui nous donne des expressions pour la dimension de E en fonction du rang de F et G ainsi que de la dimension de leurs noyaux respectifs. On utilise également la formule pour la dimension d'une somme d'espaces.
En appliquant ces formules, on obtient deux équations donnant le rang de F plus le rang de G. En combinant ces équations, on montre que le rang de F plus le rang de G est égal à la dimension de E. Cela implique que la dimension de l'intersection des noyaux est nulle, ce qui prouve que les sommes sont directes.
Cet exercice nécessite de bien connaître les formules du théorème du rang et de la dimension d'une somme d'espaces. Il est conseillé de poser les formules et de faire des calculs intermédiaires pour vérifier les résultats.