Skieur

Aujourd'hui, nous allons faire un exercice de mécanique sur un skieur. Le skieur pèse 70 kg et descend une piste rectiligne inclinée d'un certain angle alpha par rapport à l'horizontale. Il est soumis à son poids ainsi qu'à la réaction de la piste, qui se divise en une composante normale et une composante tangentielle. Tout d'abord, nous devons représenter les différentes forces sur un schéma. Le skieur est orienté vers la descente, avec son poids dirigé vers le bas et la réaction normale perpendiculaire à la piste. La composante tangentielle est dirigée dans la direction opposée au mouvement. Il est important de faire attention à ne pas confondre la réaction du support avec le frottement. 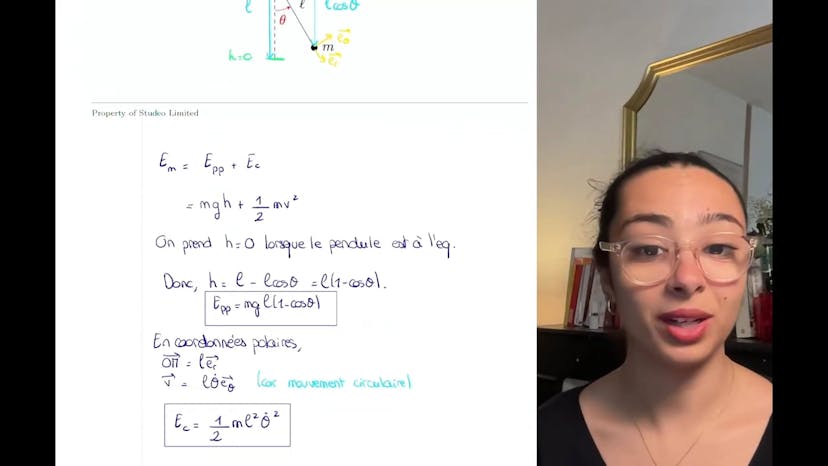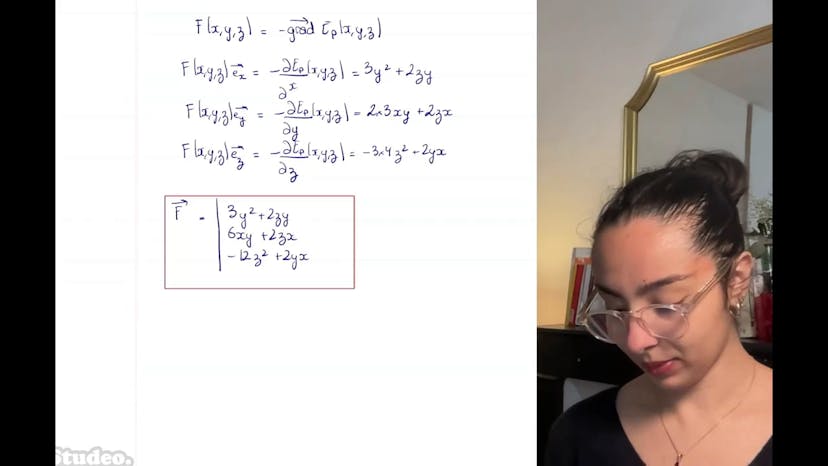Ensuite, nous devons calculer le travail de ces trois forces pendant la descente. Le travail du poids est calculé en utilisant la formule W = ∫F.ds, où F est la force du poids projetée sur la direction du déplacement élémentaire dx. Le travail du poids est donc mg.sin(α).L, où L est la longueur de la piste. Plus l'angle alpha est grand, plus le poids travaille. La réaction normale n'effectue aucun travail, car elle n'apporte aucun mouvement. Enfin, le travail de la force de frottement est calculé en utilisant la loi de Coulomb, qui indique que la force de frottement est égale au coefficient de frottement mu multiplié par la réaction normale. Le travail de la force de frottement est donc -mu.mg.cos(α).L, ce qui signifie qu'il est résistant au mouvement. 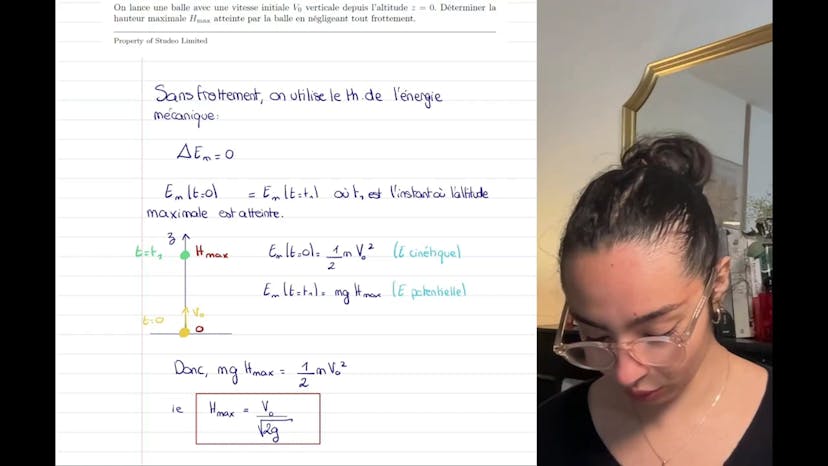Ensuite, nous devons appliquer le principe de conservation de l'énergie cinétique pour déterminer la vitesse du skieur en bas de la piste. La formule utilisée est 1/2mv² = mg.sin(α).L - mu.mg.cos(α). En résolvant cette équation, nous obtenons v = racine carrée de 2gL.sin(α) - mu.cos(α), soit environ 18 m/s ou 65 km/h. En conclusion, dans cette vidéo, nous avons appris comment calculer le travail en utilisant la formule de l'intégrale de la force scalaire du déplacement. Nous avons également utilisé le théorème de l'énergie cinétique pour calculer la vitesse en un point précis. J'espère que cela vous a été utile, n'hésitez pas à poser vos questions dans les commentaires. À bientôt !